题目内容
各棱长都等于a的四面体ABCD中,设G为BC的中点,E为△ACD内的动点(含边界),且GE∥平面ABD,若线段GE长度的最小值为
,则a的值为( )
| ||
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:直线与平面平行的判定,棱锥的结构特征
专题:空间位置关系与距离
分析:取AC中点M,CD中点N,连接GM,GN,MN,根据线面平行的判定定理可得:GM∥平面ABD,GN∥平面ABD,再结合面面平行的判定定理得到:平面GMN∥平面ABD,进而得到点E的轨迹为线段MN.从而GE为等边三角形GMN的一条高,即得a的值.
解答:
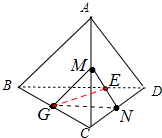 解:取AC中点M,CD中点N,连接GM,GN,MN,
解:取AC中点M,CD中点N,连接GM,GN,MN,
则GM、GN、MN分别是三角形ABC、BCD、ACD的中位线,
所以平面GMN∥平面BAD,
又四面体ABCD中各棱长都等于a,
所以△GMN为边长为
的正三角形.
取MN中点E,连结GE,则GE=
.
又GE=
=
a,
所以
=
a,即a=2.
故选:C.
 解:取AC中点M,CD中点N,连接GM,GN,MN,
解:取AC中点M,CD中点N,连接GM,GN,MN,则GM、GN、MN分别是三角形ABC、BCD、ACD的中位线,
所以平面GMN∥平面BAD,
又四面体ABCD中各棱长都等于a,
所以△GMN为边长为
| a |
| 2 |
取MN中点E,连结GE,则GE=
| ||
| 2 |
又GE=
(
|
| ||
| 4 |
所以
| ||
| 2 |
| ||
| 4 |
故选:C.
点评:本题主要考查线面平行与面面平行的判定定理,解决此题的关键是仔细审题挖掘题中隐含条件,属中档题.

练习册系列答案
相关题目
| ∫ | 2 -2 |
| A、2e2-2 |
| B、2e2 |
| C、e2-e-2 |
| D、e2+e-2-2 |
“a>b”是“a2>b2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
数列{an}是公差不为零的等差数列,其前n项和为Sn,若记数据a1,a2,a3,…,a2015的方差为λ1,数据
,
,
,…,
的方差为λ2,k=
.则( )
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| λ1 |
| λ2 |
| A、k=4. |
| B、k=2. |
| C、k=1. |
| D、k的值与公差d的大小有关. |
若复数z满足z(3-4i)=5,则z的虚部为( )
A、-
| ||
B、
| ||
| C、-4 | ||
| D、4 |