题目内容
17.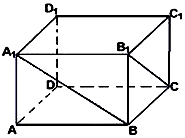 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,(1)求异面直线A1B与B1C所成角的余弦值..
(2)若点E、F分别是AB、A1B的中点,求证:EF∥平面BDD1.
分析 (1)连接A1D,将B1C平移到A1D,根据异面直线所成角的定义可知∠BA1D为异面直线A1B与B1C所成的角,在△A1DB中利用余弦定理求出此角的余弦值;
(2)连接BD1,根据EF∥DD1来证明EF∥平面BDD1.
解答 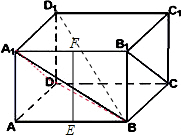 解:(1)连接A1D,
解:(1)连接A1D,
∵A1D∥B1C,
∴∠BA1D为异面直线A1B与B1C所成的角.
连接BD,在△A1DB中,A1B=A1D=5,BD=4$\sqrt{2}$,
则cos∠BA1D=$\frac{{A}_{1}{B}^{2}+{A}_{1}{D}^{2}-B{D}^{2}}{2{A}_{1}B•{A}_{1}D}$=$\frac{25+25-32}{2•5•5}$=$\frac{9}{25}$.
∴异面直线A1B与B1C所成角的余弦值为$\frac{9}{25}$;
(2)证明:∵点E、F分别是AB、A1B的中点,
∴EF∥AA1.
∵DD1∥AA1,
∴EF∥DD1,
又DD1?平面BDD1,EF?平面BDD1,
∴EF∥平面BDD1.
点评 本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
15.下列命题中错误的是( )
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,α∩β=l,过α内任意一点作l的垂线m,则m⊥β |
12.下列选项中表述正确的是( )
| A. | 空间中任意三点确定一个平面 | |
| B. | 直线上的两点和直线外的一点可以确定一个平面 | |
| C. | 分别在三条不同的直线上的三点确定一个平面 | |
| D. | 不共线的四点确定一个平面 |
2.给出下列结论:
①命题“?x∈R,sinx≠1”的否定是“?x∈R,sinx=1”;
②数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分不必要条件;
③命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中正确的是( )
①命题“?x∈R,sinx≠1”的否定是“?x∈R,sinx=1”;
②数列{an}满足“an+1=3an”是“数列{an}为等比数列”的充分不必要条件;
③命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中正确的是( )
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
6.变量x,y之间的一组相关数据如表所示:
若x,y之间的线性回归方程为$\widehaty$=$\widehatb$x+12.28,则$\widehatb$的值为( )
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.92 | B. | -0.94 | C. | -0.96 | D. | -0.98 |
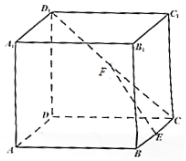 如图,在正方体ABCD-A1B1C1D1中,E、F分别是线段BC、CD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是线段BC、CD1的中点.