题目内容
5．若关于x的方程x2-x-（m+1）=0在[-1，1]上有解，则m的取值范围是[-$\frac{5}{4}$，1]．（结果写成区间形式）分析 分离参数m=x2-x-1，x∈[-1，1]．对“=”右端配方可得m的取值范围．
解答 解：由原方程得m=x2-x-1=（x-$\frac{1}{2}$）2-$\frac{5}{4}$≥-$\frac{5}{4}$；
∴x=-1时，m取最大值1；
∴m的取值范围为：[-$\frac{5}{4}$，1]．
故答案为：[-$\frac{5}{4}$，1]．
点评 考查一元二次方程解的情况和对应的二次函数与x轴交点的情况的关系，判别式的取值和二次函数与x轴交点情况的关系，要熟悉并利用二次函数的图象．
练习册系列答案
阅读快车系列答案
相关题目
3．已知函数f（x）=ax3+c，且f′（1）=6，函数在[1，2]上的最大值为20，则c的值为（ ）
| A． | 1 | B． | 4 | C． | -1 | D． | 0 |
1．在△ABC中，角A、B、C所对的边分别为a、b、c，且b（2sinB-sinA）+（2a-b）sinA=2csinC，则C=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
8．已知cos（x-$\frac{π}{4}$）=-$\frac{1}{3}$（$\frac{5π}{4}$＜x＜$\frac{7π}{4}$），则sinx-cos2x=（ ）
| A． | $\frac{5\sqrt{2}-12}{18}$ | B． | $\frac{-4\sqrt{2}-7}{9}$ | C． | $\frac{4-7\sqrt{2}}{9}$ | D． | $\frac{-4-7\sqrt{2}}{9}$ |
如图，四棱锥P-ABCD，侧面PAD是边长为4的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．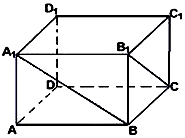
在长方体ABCD-A1B1C1D1中，已知DA=DC=4，DD1=3，