题目内容
已知a∈R，集合A={a-1，2a-1，a2+1}，B={-3，a，2}，如果A∩B={-3}，求实数a的值．
考点：交集及其运算
专题：计算题,集合
分析：由题意，-3∈{a-1，2a-1，a2+1}，讨论三个元素哪个等于-3即可．
解答：
解：∵A={a-1，2a-1，a2+1}，B={-3，a，2}，且A∩B={-3}，
∴-3∈{a-1，2a-1，a2+1}，
若a-1=-3，则a=-2，
此时A={-3，-5，5}，B={-3，-2，2}成立；
若2a-1=-3，则a=-1，
此时A={-2，-3，2}，B={-3，-1，2}，不成立；
若a2+1=-3，无解．
综上所述，a=-2．
∴-3∈{a-1，2a-1，a2+1}，
若a-1=-3，则a=-2，
此时A={-3，-5，5}，B={-3，-2，2}成立；
若2a-1=-3，则a=-1，
此时A={-2，-3，2}，B={-3，-1，2}，不成立；
若a2+1=-3，无解．
综上所述，a=-2．
点评：本题考查了集合的运算与集合的元素的互异性，属于基础题．
练习册系列答案
相关题目
设M（x0，y0）为抛物线C：y=
x2上一点，F为抛物线C的焦点，以F为圆心、|FM|为半径的圆和抛物线C的准线相交，则y0的取值范围是（ ）
| 1 |
| 8 |
| A、（2，+∞） | ||
| B、[0，2] | ||
C、（0，
| ||
D、（
|
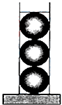圆柱形容器内盛有高度为4cm的水，若放入三个相同的铁球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图），则球的表面积是（ ）| A、2π | B、4π | C、8π | D、16π |
设A是棱长为a的正方体的一个顶点，过从此顶点出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，所得的各截面与正方体各面共同围成一个多面体，则关于此多面体有以下结论：
①有12个顶点；②有24条棱；③有12个面；④表面积为3a2；⑤体积为
a3．
其中正确的结论是（ ）
①有12个顶点；②有24条棱；③有12个面；④表面积为3a2；⑤体积为
| 5 |
| 6 |
其中正确的结论是（ ）
| A、①③④ | B、①②⑤ |
| C、②③⑤ | D、②④⑤ |
如图所示，甲、乙、丙是三个空间立体图形的三视图，甲、乙、丙对应的标号正确的是（ ）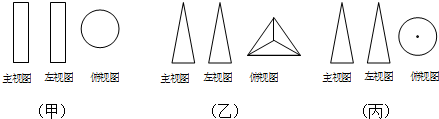
①长方体 ②圆锥 ③三棱锥 ④圆柱．
①长方体 ②圆锥 ③三棱锥 ④圆柱．
| A、③②④ | B、②①③ |
| C、①②③ | D、④③② |
若函数g（x）=x2+2x-12m在区间（-∞，-2）与（-2，1）上各有一个实根，则实数m的取值范围是（ ）
A、（-∞，
| ||
B、（
| ||
C、（0，
| ||
D、（
|