题目内容
中心城区现有绿化面积为1000hm2,计划每年增长4%,经过x(x∈N*)年,绿化面积为y hm2,则x,y间的函数关系式为( )
| A、y=1000(1+4%)x(x∈N*) |
| B、y=(1000×4%)x(x∈N*) |
| C、y=1000(1-4%)x (x∈N*) |
| D、y=1000(4%)x(x∈N*) |
考点:函数解析式的求解及常用方法
专题:计算题,应用题,函数的性质及应用
分析:由题意可知增长率问题属于指数函数问题,可以用等比数列的通项公式解决,即每年的绿化面积构成首项为1000,公比为(1+4%)的等比数列,利用等比数列的通项公式可求得x,y间的关系.
解答:
解:∵现有绿化面积1000hm2,且每年增长4%,
∴每年的绿化面积构成首项为1000,公比为(1+4%)的等比数列,设为{an},a1=1000,
∴经过x(x∈N*)年,绿化面积即为y=ax+1=1000(1+4%)x,
∴y=1000×(1+4%)x(x∈N*),
故选A.
∴每年的绿化面积构成首项为1000,公比为(1+4%)的等比数列,设为{an},a1=1000,
∴经过x(x∈N*)年,绿化面积即为y=ax+1=1000(1+4%)x,
∴y=1000×(1+4%)x(x∈N*),
故选A.
点评:本题考查函数模型在实际问题中的应用,属基础题,仔细审题,正确建立数学模型是解决问题的关键.

练习册系列答案
相关题目
已知a=(
)0.3,b=0.3-2,c=log
2,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、c>b>a |
已知函数f(x)由下表给出,则f[f(4)]等于( )
| x | 1 | 2 | 3 | 4 |
| f(x) | 3 | 2 | 4 | 1 |
| A、4 | B、3 | C、2 | D、1 |
执行如图的程序框图,若输入的x∈[0,1],则输出的x的范围是( )


| A、[1,3] |
| B、[3,7] |
| C、[7,15] |
| D、[15,31] |
已知集合A={x|x<a},B={x|2<x<4},且A∪(∁RB)=R,则实数a的取值范围( )
| A、a≤4 | B、a<2 |
| C、a>4 | D、a≥4 |
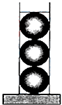 圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )
圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )| A、2π | B、4π | C、8π | D、16π |
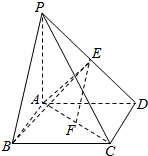 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.