题目内容
设集合S={y|y=(
)x-1,x∈R},T={y|y=log2(x+2)},S∪T=( )
| 1 |
| 2 |
| A、S | B、T |
| C、R | D、[-1,+∞) |
考点:并集及其运算
专题:集合
分析:根据(
)x>0求出集合S,由对数函数的值域求出集合T,再由并集的运算求出S∪T.
| 1 |
| 2 |
解答:
解:由y=(
)x-1、x∈R得,y>-1,则集合S={y|y>-1},
由y=log2(x+2)∈R得,集合T=R,
所以S∪T=R,
故选:C.
| 1 |
| 2 |
由y=log2(x+2)∈R得,集合T=R,
所以S∪T=R,
故选:C.
点评:本题考查并集及其运算,以及指数函数、对数函数的性质,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知函数f(x)由下表给出,则f[f(4)]等于( )
| x | 1 | 2 | 3 | 4 |
| f(x) | 3 | 2 | 4 | 1 |
| A、4 | B、3 | C、2 | D、1 |
设M(x0,y0)为抛物线C:y=
x2上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| 1 |
| 8 |
| A、(2,+∞) | ||
| B、[0,2] | ||
C、(0,
| ||
D、(
|
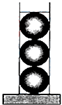 圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )
圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )| A、2π | B、4π | C、8π | D、16π |
若函数g(x)=x2+2x-12m在区间(-∞,-2)与(-2,1)上各有一个实根,则实数m的取值范围是( )
A、(-∞,
| ||
B、(
| ||
C、(0,
| ||
D、(
|
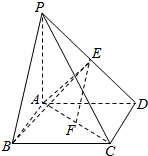 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.