题目内容
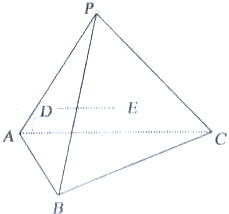
如图,三棱锥P-ABC中,D、E分别是△PAB、△PBC的重心.求证:DE∥平面ABC.

考点:直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:连接PD,PE分别与AB,BC交于M,N,则M,N是AB,BC的中点,利用D、E分别是△PAB、△PBC的重心,可得DE∥MN,根据直线与平面平行的判定定理可得结论.
解答:
 证明:连接PD,PE分别与AB,BC交于M,N,则M,N是AB,BC的中点,
证明:连接PD,PE分别与AB,BC交于M,N,则M,N是AB,BC的中点,
∵D、E分别是△PAB、△PBC的重心,
∴DE∥MN,
∵DE?平面ABC,MN?平面ABC,
∴DE∥平面ABC.
 证明:连接PD,PE分别与AB,BC交于M,N,则M,N是AB,BC的中点,
证明:连接PD,PE分别与AB,BC交于M,N,则M,N是AB,BC的中点,∵D、E分别是△PAB、△PBC的重心,
∴DE∥MN,
∵DE?平面ABC,MN?平面ABC,
∴DE∥平面ABC.
点评:本题考查直线与平面平行的判定,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
执行如图的程序框图,若输入的x∈[0,1],则输出的x的范围是( )


| A、[1,3] |
| B、[3,7] |
| C、[7,15] |
| D、[15,31] |
设M(x0,y0)为抛物线C:y=
x2上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| 1 |
| 8 |
| A、(2,+∞) | ||
| B、[0,2] | ||
C、(0,
| ||
D、(
|
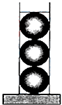 圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )
圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )| A、2π | B、4π | C、8π | D、16π |
设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
a3.
其中正确的结论是( )
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
| 5 |
| 6 |
其中正确的结论是( )
| A、①③④ | B、①②⑤ |
| C、②③⑤ | D、②④⑤ |
如图所示,甲、乙、丙是三个空间立体图形的三视图,甲、乙、丙对应的标号正确的是( )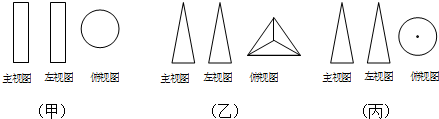
①长方体 ②圆锥 ③三棱锥 ④圆柱.

①长方体 ②圆锥 ③三棱锥 ④圆柱.
| A、③②④ | B、②①③ |
| C、①②③ | D、④③② |
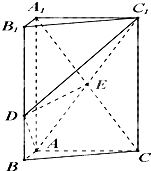 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=