题目内容

将棱长为1的正方体木块切削成一个体积最大的球，则该球的体积为（　　）
A、
π
6
B、
2
3
π
C、
4
3
π
D、
3
2
π
考点：棱柱、棱锥、棱台的体积
专题：转化思想,空间位置关系与距离
分析：将棱长为1的正方体木块切削成一个体积最大的球，结合正方体和球的结构特征，可以求出球的半径，代入球的体积公式即可求出答案．
解答： 解：将棱长为1的正方体木块切削成一个体积最大的球时，
球的直径等于正方体的棱长1，
则球的半径R=
1
2

则球的体积V=
4
3
•π•R3=
π
6

故选：A．
点评：本题考查的知识点是球的体积，其中根据正方体和圆的结构特征，求出球的半径，是解答本题的关键．
练习册系列答案
相关题目
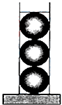圆柱形容器内盛有高度为4cm的水，若放入三个相同的铁球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图），则球的表面积是（　　）
A、2πB、4πC、8πD、16π
若函数g（x）=x2+2x-12m在区间（-∞，-2）与（-2，1）上各有一个实根，则实数m的取值范围是（　　）
A、（-∞，
1
4
）
B、（
1
4
+∞）
C、（0，
1
4
）
D、（
1
4
，1）
甲、乙两人在一次射击比赛中各射靶5次，两人成绩的条形统计图如图所示，则（　　）
A、甲的成绩的平均数小于乙的成绩的平均数
B、甲的成绩的方差小于乙的成绩的方差
C、甲的成绩的中位数等于乙的成绩的中位数
D、甲的成绩的极差小于乙的成绩的极差
已知E为不等式组
x+y≥2
x+2y≤4
y≥1
，表示区域内的一点，过点E的直线l与圆M：（x-1）2+y2=9相交于A，C两点，过点E与l垂直的直线交圆M于B、D两点，当AC取最小值时，四边形ABCD的面积为（　　）
A、12
B、6
7
C、12
2
D、4
5
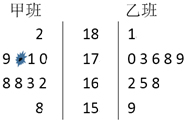随机抽取某中学高三年级甲乙两班各10名同学，测量出他们的身高（单位：cm），获得身高数据的茎叶图如图．其中甲班有一个数据被污损．
（Ⅰ）若已知甲班同学身高平均数为170cm，求污损处的数据；
（Ⅱ）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率．
画出y=x -
1
2
的函数图象．
给出如下五个结论：
①存在α∈（0，
π
2
）使sinα+cosα=
1
3

②存在区间（a，b）使y=cosx为减函数而sinx＜0
③y=tanx在其定义域内为增函数
④y=cos2x+sin（
π
2
-x）既有最大、最小值，又是偶函数
⑤y=|sin（2x+
π
6
）|最小正周期为π
其中正确结论的序号是
 
．
已知两点A（-2，1），B（1，5），点C是圆x2+y2-2x+4y-4=0上的动点，则△ABC面积的最大值为（　　）
A、35B、18C、16D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网