题目内容
设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.则∁U(A∩B)= .
考点:交、并、补集的混合运算
专题:集合
分析:根据集合的基本运算即可得到结论.
解答:
解:∵A={x|-1≤x<3},B={x|2x-4≥x-2}={x|x≥2}.
∴A∩B={x|2≤x<3},
∴∁U(A∩B)={x|x≥3或x<2}.
故答案为:(-∞,2)∪[3,+∞)
∴A∩B={x|2≤x<3},
∴∁U(A∩B)={x|x≥3或x<2}.
故答案为:(-∞,2)∪[3,+∞)
点评:本题主要考查集合的基本运算,要求熟练掌握集合的交并补运算,比较基础.

练习册系列答案
相关题目
设M(x0,y0)为抛物线C:y=
x2上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| 1 |
| 8 |
| A、(2,+∞) | ||
| B、[0,2] | ||
C、(0,
| ||
D、(
|
盒中有4个相同的球,标号1,2,3,4.现从盒中随机摸一个,若摸出球上的数字是被摸球中最大的则留下,否则放回,则5次内(包括5次)把球摸完的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
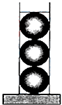 圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )
圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )| A、2π | B、4π | C、8π | D、16π |
甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则( )


| A、甲的成绩的平均数小于乙的成绩的平均数 |
| B、甲的成绩的方差小于乙的成绩的方差 |
| C、甲的成绩的中位数等于乙的成绩的中位数 |
| D、甲的成绩的极差小于乙的成绩的极差 |
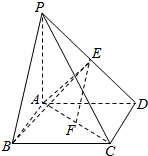 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.