题目内容
对于c>0,当非零实数a,b满足4a2-2ab+b2-c=0且使|2a+b|最大时,
+
+
的最小值为 .
| 1 |
| a |
| 2 |
| b |
| 4 |
| c |
考点:一般形式的柯西不等式,基本不等式
专题:不等式的解法及应用
分析:首先把:4a2-2ab+b2-c=0,转化为
=(a-
)2+
b2,再由柯西不等式得到|2a+b|2,分别用b表示a,c,在代入到
+
+
得到关于b的二次函数,求出最小值即可.
| c |
| 4 |
| b |
| 4 |
| 3 |
| 16 |
| 1 |
| a |
| 2 |
| b |
| 4 |
| c |
解答:
解:∵4a2-2ab+b2-c=0,
∴
=(a-
)2+
b2
由柯西不等式得,
[(a-
)2+(
)2][22+(2
)2]≥[2(a-
)+
×2
]2=|2a+b|2
故当|2a+b|最大时,有
=
∴a=
b,c=b2
∴
+
+
=
+
+
=4(
+
)2-1
当b=-2时,取得最小值为-1.
故答案为:-1
∴
| c |
| 4 |
| b |
| 4 |
| 3 |
| 16 |
由柯西不等式得,
[(a-
| b |
| 4 |
| ||
| 4 |
| 3 |
| b |
| 2 |
| ||
| 4 |
| 3 |
故当|2a+b|最大时,有
a-
| ||
| 2 |
| ||||
2
|
∴a=
| 1 |
| 2 |
∴
| 1 |
| a |
| 2 |
| b |
| 4 |
| c |
| 2 |
| b |
| 2 |
| b |
| 4 |
| b2 |
| 1 |
| b |
| 1 |
| 2 |
当b=-2时,取得最小值为-1.
故答案为:-1
点评:本题考查了柯西不等式,以及二次函数的最值问题,属于难题.

练习册系列答案
相关题目
已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
A、-
| ||
| B、-1 | ||
C、-
| ||
D、-
|
某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
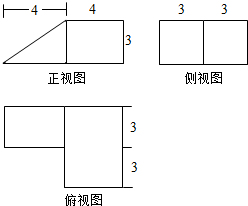

| A、72cm3 |
| B、90cm3 |
| C、108cm3 |
| D、138cm3 |