题目内容
若函数f(x)=cos2x+asinx在区间(
,
)是减函数,则a的取值范围是 .
| π |
| 6 |
| π |
| 2 |
考点:复合三角函数的单调性
专题:函数的性质及应用,三角函数的图像与性质
分析:利用二倍角的余弦公式化为正弦,然后令t=sinx换元,根据给出的x的范围求出t的范围,结合二次函数的图象的开口方向及对称轴的位置列式求解a的范围.
解答:
解:由f(x)=cos2x+asinx
=-2sin2x+asinx+1,
令t=sinx,
则原函数化为y=-2t2+at+1.
∵x∈(
,
)时f(x)为减函数,
则y=-2t2+at+1在t∈(
,1)上为减函数,
∵y=-2t2+at+1的图象开口向下,且对称轴方程为t=
.
∴
≤
,解得:a≤2.
∴a的取值范围是(-∞,2].
故答案为:(-∞,2].
=-2sin2x+asinx+1,
令t=sinx,
则原函数化为y=-2t2+at+1.
∵x∈(
| π |
| 6 |
| π |
| 2 |
则y=-2t2+at+1在t∈(
| 1 |
| 2 |
∵y=-2t2+at+1的图象开口向下,且对称轴方程为t=
| a |
| 4 |
∴
| a |
| 4 |
| 1 |
| 2 |
∴a的取值范围是(-∞,2].
故答案为:(-∞,2].
点评:本题考查复合函数的单调性,考查了换元法,关键是由换元后函数为减函数求得二次函数的对称轴的位置,是中档题.

练习册系列答案
相关题目
要制作一个容积为4m3,高为1m的无盖长方体容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )
| A、80元 | B、120元 |
| C、160元 | D、240元 |
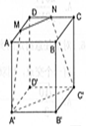 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题: