题目内容
(
-
)8的展开式中x2y2的系数为 .(用数字作答)
| x | ||
|
| y | ||
|
考点:二项式定理
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x、y的幂指数都等于2,求得r的值,即可求得展开式中x2y2的系数.
解答:
解:(
-
)8的展开式的通项公式为 Tr+1=
•(-1)r•(
)8-r•(
)r=
•(-1)r•x8-
•y
-4,
令 8-
=
-4=2,求得 r=4,
故展开式中x2y2的系数为
=70,
故答案为:70.
| x | ||
|
| y | ||
|
| C | r 8 |
| x | ||
|
| y | ||
|
| C | r 8 |
| 3r |
| 2 |
| 3r |
| 2 |
令 8-
| 3r |
| 2 |
| 3r |
| 2 |
故展开式中x2y2的系数为
| C | 4 8 |
故答案为:70.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为
和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
. |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)在x=x0处导数存在,若p:f′(x0)=0:q:x=x0是f(x)的极值点,则( )
| A、p是q的充分必要条件 |
| B、p是q的充分条件,但不是q的必要条件 |
| C、p是q的必要条件,但不是q的充分条件 |
| D、p既不是q的充分条件,也不是q的必要条件 |
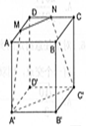 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题: