题目内容
已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
A、-
| ||
| B、-1 | ||
C、-
| ||
D、-
|
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用点A(-2,3)在抛物线C:y2=2px的准线上,确定焦点F的坐标,即可求出直线AF的斜率.
解答:
解:∵点A(-2,3)在抛物线C:y2=2px的准线上,
∴-
=-2,
∴F(2,0),
∴直线AF的斜率为
=-
.
故选:C.
∴-
| p |
| 2 |
∴F(2,0),
∴直线AF的斜率为
| 3 |
| -2-2 |
| 3 |
| 4 |
故选:C.
点评:本题考查抛物线的性质,考查直线斜率的计算,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=cos(2x-
)的最小正周期是( )
| π |
| 6 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为
和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
. |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=2-i,则z•
的值为( )
. |
| z |
| A、5 | ||
B、
| ||
| C、3 | ||
D、
|
要制作一个容积为4m3,高为1m的无盖长方体容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )
| A、80元 | B、120元 |
| C、160元 | D、240元 |
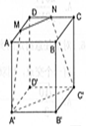 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题: