题目内容
16.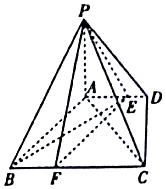 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.(Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)若△PBC的面积是梯形ABCD面积的$\frac{4}{3}$,求点E到平面PBC的距离.
分析 (Ⅰ)已知点F在BC上,且CF=2FB,证明EF⊥平面PAC,即可证明:平面PEF⊥平面PAC;
(Ⅱ)E到平面PBC的距离即时A到平面PBC的距离,利用VA-PBC=VP-ABC,求点E到平面PBC的距离.
解答  (Ⅰ)证明:∵AB⊥AC,AB=AC,∴∠ACB=45°,
(Ⅰ)证明:∵AB⊥AC,AB=AC,∴∠ACB=45°,
∵底面ABCD是直角梯形,∠ADC=90°,AD∥BC,
∴∠ACD=45°,即AD=CD,
∴$BC=\sqrt{2}AC=2AD$,
∵AE=2ED,CF=2FB,∴$AE=BF=\frac{2}{3}AD$,
∴四边形ABFE是平行四边形,则AB∥EF,
∴AC⊥EF,
∵PA⊥底面ABCD,∴PA⊥EF,
∵PA∩AC=A,
∴EF⊥平面PAC,∵EF?平面PEF,
∴平面PEF⊥平面PAC.
(Ⅱ)解:∵PA⊥底面ABCD,且AB=AC,∴PB=PC,
取BC的中点为G,连接AG,则AG⊥BC,AG=CD=1
设PA=x,连接PG,则$PG=\sqrt{{x^2}+1}$,
∵侧面PBC的面积是底面ABCD的$\frac{4}{3}$倍,
∴$\frac{1}{2}×2•PG=\frac{4}{3}×\frac{1}{2}×(1+2)$,即PG=2,求得$x=\sqrt{3}$,
∵AD∥BC,∴E到平面PBC的距离即时A到平面PBC的距离,
∵VA-PBC=VP-ABC,S△PBC=2S△ABC,
∴E到平面PBC的距离为$\frac{1}{2}PA=\frac{{\sqrt{3}}}{2}$.
点评 本题考查线面垂直、面面垂直的证明,考查点到平面的距离的求法,是中档题,

练习册系列答案
相关题目
6.已知集合A={x|x2-2x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|-1≤x≤1} | D. | {x|-2≤x≤-1} |
7.已知向量$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(t,2),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则|$\overrightarrow{m}$+$\overrightarrow{n}$|=( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
4.已知抛物线x2=4y上一点A纵坐标为4,则点A到抛物线焦点的距离为( )
| A. | $\sqrt{10}$ | B. | 4 | C. | 5 | D. | $\sqrt{15}$ |
8.已知直线l1:mx+3y+3=0,l2:x+(m-2)y+1=0,则“m=3”是“l1∥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知函数f(x)=2cos(ωx+$\frac{3}{2}$π)(ω>0)的最小正周期为2π,则函数f(x)图象的一条对称轴方程为( )
| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{3}{4}$π | D. | x=π |