题目内容
17．已知函数$f（x）=\left\{\begin{array}{l}2a-x，x≤0\\{log_a}x，x＞0\end{array}\right.$（a＞0且a≠1），若f（f（1））=1，则a=$\frac{1}{2}$．分析 先求出f（1）=loga1=0，再由f（f（1））=1，得f（f（1））=f（0）=2a-0=1，由此能求出a．
解答 解：∵函数$f（x）=\left\{\begin{array}{l}2a-x，x≤0\\{log_a}x，x＞0\end{array}\right.$（a＞0且a≠1），
∴f（1）=loga1=0，
∵f（f（1））=1，
∴f（f（1））=f（0）=2a-0=1，
解得a=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
7．已知实数a，b满足2＜a＜b＜3，下列不等关系中一定成立的是（ ）
| A． | a3+15b＞b3+15a | B． | a3+15b＜b3+15a | C． | b•2a＞a•2b | D． | b•2a＜a•2b |
12．
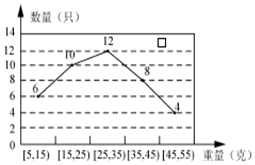某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：
（1）记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；
（2）若购进这批小龙虾100千克，试估计这批小龙虾的数量；
（3）为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：
按分层抽样抽取10只，再随机抽取3只品尝，记X为抽到二等品的数量，求抽到二级品的期望．
某经销商从外地水产养殖厂购进一批小龙虾，并随机抽取40只进行统计，按重量分类统计结果如图：（1）记事件A为：“从这批小龙虾中任取一只，重量不超过35g的小龙虾”，求P（A）的估计值；
（2）若购进这批小龙虾100千克，试估计这批小龙虾的数量；
（3）为适应市场需求，了解这批小龙虾的口感，该经销商将这40只小龙虾分成三个等级，如下表：
| 等级 | 一等品 | 二等品 | 三等品 |
| 重量（g） | [5，25） | [25，45） | [45，55] |
2．
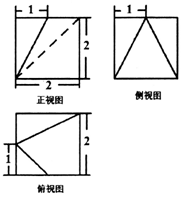如图为一个多面体的三视图，则该多面体的体积为（ ）
如图为一个多面体的三视图，则该多面体的体积为（ ）| A． | $\frac{20}{3}$ | B． | 7 | C． | $\frac{22}{3}$ | D． | $\frac{23}{3}$ |
6．已知集合A={x|x2-2x-3≥0}，B={x|-2≤x≤2}，则A∩B=（ ）
| A． | {x|1≤x≤2} | B． | {x|-1≤x≤2} | C． | {x|-1≤x≤1} | D． | {x|-2≤x≤-1} |
7．已知向量$\overrightarrow{m}$=（-1，1），$\overrightarrow{n}$=（t，2），若$\overrightarrow{m}$⊥$\overrightarrow{n}$，则|$\overrightarrow{m}$+$\overrightarrow{n}$|=（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{5}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{10}$ |