题目内容
15.若实数x,y满足约束条件$\left\{\begin{array}{l}x≥0\;\\ y≤x\;\\ x+y+a≤0\;\end{array}\right.$且z=x+3y的最大值为4,则实数a的值为-2.分析 作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到a的值.
解答 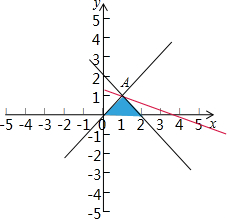 解:不等式组约束条件$\left\{\begin{array}{l}x≥0\;\\ y≤x\;\\ x+y+a≤0\;\end{array}\right.$对应的平面区域如图:
解:不等式组约束条件$\left\{\begin{array}{l}x≥0\;\\ y≤x\;\\ x+y+a≤0\;\end{array}\right.$对应的平面区域如图:
由z=x+3y得y=-$\frac{1}{3}$x+$\frac{1}{3}$z,
平移直线y=-$\frac{1}{3}$x+$\frac{1}{3}$z,则由图象可知当直线y=-$\frac{1}{3}$x+$\frac{1}{3}$z经过点A时直线y=-$\frac{1}{3}$x+$\frac{1}{3}$z的截距最大,
此时z最大,为x+3y=4
由$\left\{\begin{array}{l}{x=y}\\{x+3y=4}\end{array}\right.$,
解得A(1,1),
此时点A在x+y+a=0上,
即2+a=0,
解得a=-2
故答案为:-2.
点评 本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知集合A={x|x2-2x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|-1≤x≤1} | D. | {x|-2≤x≤-1} |
10.已知集合A={x|1≤x≤4},B={x|x>2},那么A∪B=( )
| A. | (2,4) | B. | (2,4] | C. | [1,+∞) | D. | (2,+∞) |
20.在等差数列{an}中,若a6+a8+a10=72,则2a10-a12的值为( )
| A. | 20 | B. | 22 | C. | 24 | D. | 28 |
7.已知向量$\overrightarrow{m}$=(-1,1),$\overrightarrow{n}$=(t,2),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则|$\overrightarrow{m}$+$\overrightarrow{n}$|=( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
4.已知抛物线x2=4y上一点A纵坐标为4,则点A到抛物线焦点的距离为( )
| A. | $\sqrt{10}$ | B. | 4 | C. | 5 | D. | $\sqrt{15}$ |
5.已知函数f(x)=2cos(ωx+$\frac{3}{2}$π)(ω>0)的最小正周期为2π,则函数f(x)图象的一条对称轴方程为( )
| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{3}{4}$π | D. | x=π |