题目内容
已知a,b均为正数,且a+b=1,求证:
+
≤2
.
| 1+2a |
| 1+2b |
| 2 |
考点:不等式的证明
专题:推理和证明
分析:直接利用分析法的证明步骤,逐步找出使得结论成立的充分条件,a+b=1,即可.
解答:
证明:要证明
+
≤2
只需证:(
+
)2≤8…(6分)
即证:2+2(a+b)+2
≤8,
∵a+b=1
亦即证:
≤2…(10分)
∵
≤
=1+a+b=2…(14分)
故原不等式成立.
注:其他证法正确同样给分.
| 1+2a |
| 1+2b |
| 2 |
只需证:(
| 1+2a |
| 1+2b |
即证:2+2(a+b)+2
| (1+2a)(1+2b) |
∵a+b=1
亦即证:
| (1+2a)(1+2b) |
∵
| (1+2a)(1+2b) |
| (1+2a)+(1+2b) |
| 2 |
故原不等式成立.
注:其他证法正确同样给分.
点评:本题考查分析法证明不等式的方法,注意分析法的证明步骤,考查逻辑推理能力.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
在长为6cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC,BC的长,则该矩形面积小于8cm2,的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
,
满足:|
|=3,|
|=2,|
+
|=4,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
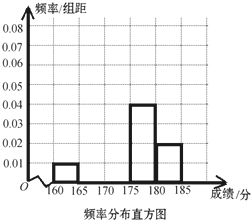 永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示:
永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示: