题目内容
若sina，cosa是关于x的方程8x2+6kx+2k+1=0的两个实根，试求k的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由题意，利用韦达定理得到sinα+cosα=-
，sinαcosα=
，根据sin2α+cos2α=1列出关于k的方程，求出方程的解即可得到k的值．
| 3k |
| 4 |
| 2k+1 |
| 8 |
解答：
解：∵sinα，cosα是关于x的方程8x2+6kx+2k+1=0的两个实根，
∴sinα+cosα=-
，sinαcosα=
，
∵sin2α+cos2α=1，
∴（sinα+cosα）2-2sinαcosα=1，即
-
=1，
整理得：（k-2）（9k+10）=0，
解得：k=2或k=-
，
∵方程有实数根，
∴△=36k2-32（2k+1）≥0，即k≤
或k≥
，
则k的值为2或-
．
∴sinα+cosα=-
| 3k |
| 4 |
| 2k+1 |
| 8 |
∵sin2α+cos2α=1，
∴（sinα+cosα）2-2sinαcosα=1，即
| 9k2 |
| 16 |
| 2k+1 |
| 4 |
整理得：（k-2）（9k+10）=0，
解得：k=2或k=-
| 10 |
| 9 |
∵方程有实数根，
∴△=36k2-32（2k+1）≥0，即k≤
| 2 |
| 3 |
| 4 |
| 3 |
则k的值为2或-
| 10 |
| 9 |
点评：此题考查了同角三角函数间基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知一个几何体的三视图是三个全等的边长为l的正方形，如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
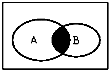已知全集U为实数集，集合 A={x|x2-2x-3＜0}，B={x|y=ln（1-x）}，则如图中阴影部分表示的集合为（ ）| A、{x|x-1≤x＜3} |
| B、{x|x＜3} |
| C、{x|x≤-1} |
| D、{x|-1＜x＜1} |