Question

已知H为锐角△ABC的垂心，PH⊥平面ABC，∠BPC=90°，求证：∠BPA=90°，∠APC=90°．

Answer 1

考点：三角形中的几何计算

专题：空间位置关系与距离

分析：延长BH交AC于F，延长CH交AB于E，先通过线面垂直的判定定理证明出PB⊥平面APC，根据线面垂直的性质证明出PB⊥AP，从而可得∠BPA=90°．同理AP⊥平面PBC，从而有AP⊥PC，即∠APC=90°．

解答：
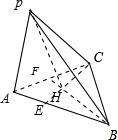
证明：延长BH交AC于F，延长CH交AB于E，
∵AC⊥BF，AC⊥PH
∴AC⊥平面PHF，
∵PB?平面PHF，
∴AC⊥PB
又∵∠BPC=90°即PB⊥PC
∴PB⊥平面APC
∵AP?平面APC
∴PB⊥AP
∴∠BPA=90°．
同理可证，CB⊥AH，CB⊥PH，
∴CB⊥AP，
又∵AP⊥BP，
∴AP⊥平面PBC，从而有AP⊥PC，即∠APC=90°．

点评：本题主要考查了线面垂直的判定定理和线面垂直的性质．要求学生对基础定理能熟练记忆并灵活运用，属于基础知识的考查．