题目内容
 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.(1)求证:D1F⊥平面AED;
(2)求平面AED与平面A1ED1所成锐二面角的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定,二面角的平面角及求法
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明D1F⊥AE,AD⊥D1F,即可证明D1F⊥平面ADE;
(2)建立直角坐标系,求出平面A1ED1的法向量、平面AED的一个法向量,利用向量的夹角公式,即可求出平面AED与平面A1ED1所成锐二面角的余弦值.
(2)建立直角坐标系,求出平面A1ED1的法向量、平面AED的一个法向量,利用向量的夹角公式,即可求出平面AED与平面A1ED1所成锐二面角的余弦值.
解答:
 (1)证明:取AB中点G,连接A1G,FG.
(1)证明:取AB中点G,连接A1G,FG.
因为F是CD的中点,所以GF、AD平行且相等,
又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F.
因为△A1AG≌△ABE,所以A1G⊥AE,
所以D1F⊥AE.
因为AC1是正方体,
所以AD⊥面DC1.
又D1F?面DC1,
所以AD⊥D1F.
因为AD∩AE=A,
所以D1F⊥平面ADE;
(2)建立如图所示的直角坐标系,D(0,0,0),A(1,0,0),D1(0,0,1),E(1,1,
),F(0,
,0),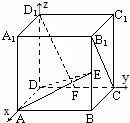
则
=(1,1,-
),
=(1,0,0),
设平面A1ED1的法向量为
=(x,y,z),则
,令z=2,则
=(0,1,2),
由(1)知,平面AED的一个法向量为
=(0,
,-1),
所以平面AED与平面A1ED1所成锐二面角的余弦值为|
|=
.
 (1)证明:取AB中点G,连接A1G,FG.
(1)证明:取AB中点G,连接A1G,FG.因为F是CD的中点,所以GF、AD平行且相等,
又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F.
因为△A1AG≌△ABE,所以A1G⊥AE,
所以D1F⊥AE.
因为AC1是正方体,
所以AD⊥面DC1.
又D1F?面DC1,
所以AD⊥D1F.
因为AD∩AE=A,
所以D1F⊥平面ADE;
(2)建立如图所示的直角坐标系,D(0,0,0),A(1,0,0),D1(0,0,1),E(1,1,
| 1 |
| 2 |
| 1 |
| 2 |

则
| D1E |
| 1 |
| 2 |
| D1A1 |
设平面A1ED1的法向量为
| n |
|
| n |
由(1)知,平面AED的一个法向量为
| D1F |
| 1 |
| 2 |
所以平面AED与平面A1ED1所成锐二面角的余弦值为|
| ||||||
|
| 3 |
| 5 |
点评:本题考查线面垂直,考查平面AED与平面A1ED1所成锐二面角的余弦值,考查逻辑推理能力和空间想象能力,属于中档题.

练习册系列答案
相关题目
| 3-2i |
| 2+3i |
A、
| ||
B、
| ||
| C、-i | ||
| D、i |
函数y=
的定义域是( )
| 2x-5 |
A、{x|x≤
| ||
B、{x|x<
| ||
C、{x|x≥
| ||
D、{x|x>
|




 如图,平行光线与水平地面成30°角,已知足球在地面上的影子是椭圆形,则该椭圆的离心率为
如图,平行光线与水平地面成30°角,已知足球在地面上的影子是椭圆形,则该椭圆的离心率为