题目内容
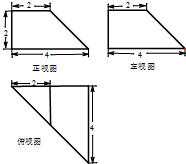 某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )
某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图知几何体为三棱台,且棱台的里面侧面与底面垂直,其中一条侧棱与底面垂直,其直观图如图,可得三个侧面都为直角梯形,底面为等腰直角三角形,
求得CC1,A1B1,AB的长,把数据代入棱台的侧面积公式与底面面积公式计算.
求得CC1,A1B1,AB的长,把数据代入棱台的侧面积公式与底面面积公式计算.
解答:
解:由三视图知几何体为三棱台,且棱台的里面侧面与底面垂直,其中一条侧棱与底面垂直,其直观图如图:

AA1⊥AB,AA1⊥AC,又BC⊥AC,∴BC⊥CC1,
∴CC1=2
,A1B1=2
,AB=4
.
∴棱台的侧面积为
×2+
×2
+
×2=6+12
,
两底面都是等腰直角三角形,其面积为
×2×2+
×4×4=10.
∴几何体的表面积S=10+6+12
=16+12
.
故选B.

AA1⊥AB,AA1⊥AC,又BC⊥AC,∴BC⊥CC1,
∴CC1=2
| 2 |
| 2 |
| 2 |
∴棱台的侧面积为
| 2+4 |
| 2 |
| 2+4 |
| 2 |
| 2 |
2
| ||||
| 2 |
| 2 |
两底面都是等腰直角三角形,其面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴几何体的表面积S=10+6+12
| 2 |
| 2 |
故选B.
点评:本题考查了由三视图求几何体的表面积,解题的关键是判断几何体的形状及求相关几何量的数据.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
等差数列{an}中,a2=4,a3+a7=20,则a8=( )
| A、8 | B、12 | C、16 | D、24 |
若集合A满足:对任意x∈A,都有
∈A,就称A是和谐集合.则在集合M={-1,0,
,
,
,1,2,3,4,5,6}的所有非空子集中,和谐集合有( )个.
| 1 |
| x |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、255 | B、127 |
| C、63 | D、31 |
设α,β,γ为两两不重合的平面,m,n为两条不重合的直线,给出下列四个命题:
①若α⊥γ,β∥γ,则α⊥β;
②若α∥γ,β∥γ,则α∥β;
③若m∥α,n∥α,则m∥n;
④若α⊥γ,β⊥γ,α∩β=m,则m⊥γ;
其中真命题的个数是( )
①若α⊥γ,β∥γ,则α⊥β;
②若α∥γ,β∥γ,则α∥β;
③若m∥α,n∥α,则m∥n;
④若α⊥γ,β⊥γ,α∩β=m,则m⊥γ;
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
在△ABC中,a、b、c分别为内角A、B、C的对边,且(a2+b2)sin(A-B)=(a2+b2)sin(A+B),则△ABC是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |