题目内容

等差数列{an}中，a2=4，a3+a7=20，则a8=（　　）
A、8B、12C、16D、24
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：直接由等差数列的性质结合已知条件列式计算．
解答： 解：∵数列{an}是等差数列，由等差数列的性质得：a2+a8=a3+a7，
又a2=4，a3+a7=20，
∴a8=a3+a7-a2=20-4=16．
故选：C．
点评：本题考查了等差数列的通项公式，考查了等差数列的性质，是基础的计算题．
练习册系列答案
相关题目
一个四棱锥的三视图如图所示，其中主视图是腰长为1的等腰直角三角形，则这个几何体的体积是
 
．
函数f（x）=
x2-2x+4
x
（x＞0）的值域是
 
．
若a=log0.40.3，b=log54，c=log20.8，则a，b，c由小到大的顺序是
 
．
函数f（x）=sin（x+φ）+cos（x+φ）为奇函数，则φ的一个可能取值（　　）
A、0
B、
π
3
C、-
π
4
D、-
π
3
已知集合A={-3，-1，0}，B={-7，-4，5，6}，从两个集合中各取一个元素作为点的坐标，则表示不在第一、二象限内的点的个数为（　　）
A、12B、14C、18D、20
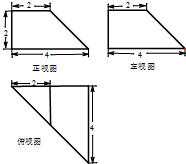某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形．则该几何体的表面积为（　　）
A、6+12
2
B、16+12
2
C、6+12
3
D、16+12
3
已知：f（x）=sin（x+
π
2
），在△ABC中，a、b、c分别为∠ABC的对边，已知a=1，b=
2
，f（A）=
3
2
，求∠C．
已知函数f（x）=axlnx（a为非零常数）图象上点（e，f（e））处的切线与直线y=2x平行（其中e=2.71828…）．
（Ⅰ）求函数f（x）解析式；
（Ⅱ）求函数f（x）在[t，2t]（t＞0）上的最小值；
（Ⅲ）若斜率为k的直线与曲线y=f'（x）交于A（x1，y1）、B（x2，y2）（x1＜x2）两点，求证：x1＜
1
k
＜x2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网