题目内容
已知O为四边形ABCD所在平面外一点，且向量
，
，
，
满足
+
=
+
，则四边形的形状为 ．
| OA |
| OB |
| OC |
| OD |
| OA |
| OC |
| OB |
| OD |
考点：向量的三角形法则
专题：平面向量及应用
分析：由于满足
+
=
+
，利用向量的三角形法则可得
-
=
-
，于是
=
，根据向量相等的意义和平行四边形的判定定理即可得出．
| OA |
| OC |
| OB |
| OD |
| OA |
| OB |
| OD |
| OC |
| BA |
| CD |
解答：
解：∵满足
+
=
+
，∴
-
=
-
，
∴
=
，
因此四边形ABCD为平行四边形．
故答案为：平行四边形．
| OA |
| OC |
| OB |
| OD |
| OA |
| OB |
| OD |
| OC |
∴
| BA |
| CD |
因此四边形ABCD为平行四边形．
故答案为：平行四边形．
点评：本题考查了向量的三角形法则、向量相等的意义和平行四边形的判定定理，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
函数f（x）=sin（x+φ）+cos（x+φ）为奇函数，则φ的一个可能取值（ ）
| A、0 | ||
B、
| ||
C、-
| ||
D、-
|
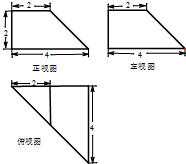某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形．则该几何体的表面积为（ ）A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|