题目内容
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(
,3).若函数f(x)=2sinα•cos2ωx+4cosα•sinωx•cosωx的图象关于直线x=
对称,其中ω为常数,且ω∈(0,1).
(1)求f(x)的表达式及其最小正周期;
(2)若将y=f(x)图象上各点的横坐标变为原来的
,再将所得图象向右平移
个单位,纵坐标不变,得到y=h(x)的图象,设函数g(x)对任意x∈R,有g(x+
)=g(x),且当x∈[0,
]时,g(x)=
-h(x),求函数g(x)在[-π,0]上的解析式.
(3)设(2)中所求得函数g(x),可使不等式g2(x)+4g(x)-a≥2x对任意x∈[-
,0]恒成立,求实数a的取值范围.
| 3 |
| π |
| 2 |
(1)求f(x)的表达式及其最小正周期;
(2)若将y=f(x)图象上各点的横坐标变为原来的
| 1 |
| 6 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
(3)设(2)中所求得函数g(x),可使不等式g2(x)+4g(x)-a≥2x对任意x∈[-
| π |
| 12 |
考点:三角函数的最值,三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:综合题,函数的性质及应用
分析:(1)依题意,可求得f(x)=2sin(2ωx+
),y=f(x)的图象关于直线x=
对称⇒f(0)=f(π)⇒sin(2πω+
)=
,而ω∈(0,1),可求得ω=
,从而可得f(x)的表达式及其最小正周期;
(2)利用函数y=Asin(ωx+φ)的图象变换可求得h(x)=2sin(2x-
),易知g(x)是以
为周期的函数,从而由当x∈[0,
]时,g(x)=
-h(x),即可求得函数g(x)在[-π,0]上的解析式;
(3)令h(x)=2x,不等式g2(x)+4g(x)-a≥2x对任意x∈[-
,0]恒成立?g2(x)+4g(x)-a≥h(x)max=h(0)=1恒成立,转化为a≤g2(x)+4g(x)-1(g(x)∈[-
,
-
])恒成立,从而可求得实数a的取值范围.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 6 |
(2)利用函数y=Asin(ωx+φ)的图象变换可求得h(x)=2sin(2x-
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
(3)令h(x)=2x,不等式g2(x)+4g(x)-a≥2x对任意x∈[-
| π |
| 12 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
解答:
解:(1)依题意知,sinα=
=
,cosα=
,
∴f(x)=2sinα•cos2ωx+4cosα•sinωx•cosωx
=
cos2ωx+sin2ωx
=2(
cos2ωx+
sin2ωx)
=2sin(2ωx+
),
又y=f(x)的图象关于直线x=
对称,
∴f(0)=f(π),即2×
=2sin(2πω+
),
∴sin(2πω+
)=
,
∵ω∈(0,1),
∴
<2πω+
<
,
∴2πω+
=
,
解得:ω=
,
∴f(x)=2sin(
x+
),T=6π;
(2)将f(x)=2sin(
x+
)图象上各点的横坐标变为原来的
,得到y=2sin(2x+
)的图象,再将所得图象向右平移
个单位,纵坐标不变,得到y=h(x)=2sin[2(x-
)+
]=2sin(2x-
),
∵函数g(x)对任意x∈R,有g(x+
)=g(x),
∴g(x)是以
为周期的函数,
又当x∈[0,
]时,g(x)=
-h(x)=
-2sin(2x-
),
∴当x∈[-
,0]时,x+
∈[0,
],g(x)=g(x+
)=
-2sin[2(x+
)-
]=
-2sin(2x+
);
当x∈∈[-π,-
]时,x+π∈[0,
],g(x)=g(x+π)=
-2sin[2(x+π)-
]=
-2sin(2x-
),
∴g(x)=
;
(3)令h(x)=2x,则h(x)=2x为增函数,
∴当x∈[-
,0]时,h(x)max=h(0)=1,
∴不等式g2(x)+4g(x)-a≥2x对任意x∈[-
,0]恒成立?g2(x)+4g(x)-a≥h(x)max=h(0)=1恒成立,
∴a≤g2(x)+4g(x)-1.
∵当x∈[-
,0]时,g(x)=
-2sin(2x+
),
由2x+
∈[
,
]知,
≤2sin(2x+
)≤2,-
≤
-2sin(2x+
)≤
-
,
即x∈[-
,0]时,g(x)=
-2sin(2x+
)∈[-
,
-
],
令t=g(x)=
-2sin(2x+
),则t∈[-
,
-
],
∴a≤g2(x)+4g(x)-1转化为:a≤t2+4t-1=(t+2)2-5(t∈[-
,
-
])恒成立;
令k(t)=(t+2)2-5(t∈[-
,
-
]),
则k(t)=(t+2)2-5在区间[-
,
-
]上单调递增,
∴k(t)min=k(-
)=-
.
∴实数a的取值范围为(-∞,-
].
| 3 | ||||
|
| ||
| 2 |
| 1 |
| 2 |
∴f(x)=2sinα•cos2ωx+4cosα•sinωx•cosωx
=
| 3 |
=2(
| ||
| 2 |
| 1 |
| 2 |
=2sin(2ωx+
| π |
| 3 |
又y=f(x)的图象关于直线x=
| π |
| 2 |
∴f(0)=f(π),即2×
| ||
| 2 |
| π |
| 3 |
∴sin(2πω+
| π |
| 3 |
| ||
| 2 |
∵ω∈(0,1),
∴
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
∴2πω+
| π |
| 3 |
| 2π |
| 3 |
解得:ω=
| 1 |
| 6 |
∴f(x)=2sin(
| 1 |
| 3 |
| π |
| 3 |
(2)将f(x)=2sin(
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵函数g(x)对任意x∈R,有g(x+
| π |
| 2 |
∴g(x)是以
| π |
| 2 |
又当x∈[0,
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴当x∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
当x∈∈[-π,-
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
∴g(x)=
|
(3)令h(x)=2x,则h(x)=2x为增函数,
∴当x∈[-
| π |
| 12 |
∴不等式g2(x)+4g(x)-a≥2x对任意x∈[-
| π |
| 12 |
∴a≤g2(x)+4g(x)-1.
∵当x∈[-
| π |
| 12 |
| 1 |
| 2 |
| 2π |
| 3 |
由2x+
| 2π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 3 |
即x∈[-
| π |
| 12 |
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
令t=g(x)=
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
∴a≤g2(x)+4g(x)-1转化为:a≤t2+4t-1=(t+2)2-5(t∈[-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
令k(t)=(t+2)2-5(t∈[-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
则k(t)=(t+2)2-5在区间[-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
∴k(t)min=k(-
| 3 |
| 2 |
| 19 |
| 4 |
∴实数a的取值范围为(-∞,-
| 19 |
| 4 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查函数的周期性与单调性,考查函数解析式的确定与函数恒成立问题,考查抽象思维与综合应用能力,属于难题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
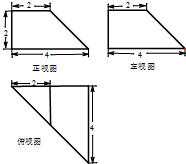 某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )
某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|