题目内容
若集合A满足:对任意x∈A,都有
∈A,就称A是和谐集合.则在集合M={-1,0,
,
,
,1,2,3,4,5,6}的所有非空子集中,和谐集合有( )个.
| 1 |
| x |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、255 | B、127 |
| C、63 | D、31 |
考点:元素与集合关系的判断
专题:
分析:根据条件分别判断集合中元素之间的关系,利用集合子集关系即可得到结论.
解答:
解:根据和谐集合的定义可知,当x=1,
=1,
当x=-1,则
=-1,
当x=2,则
=
,
当x=3,则
=
,
当x=4,则
=
不存在,
当x=5,则
=
,
当x=6,则
=
不存在,
当x=0,则
无意义,
即{1},{-1},{2,
},{3,
},{5,
}必须分别在一起,把它们分别看做一个元素的话,则和谐集合中最多含有5个,最小含有1个元素,
即和谐集合有25-1=31个,
故选:D.
| 1 |
| x |
当x=-1,则
| 1 |
| x |
当x=2,则
| 1 |
| x |
| 1 |
| 2 |
当x=3,则
| 1 |
| x |
| 1 |
| 3 |
当x=4,则
| 1 |
| x |
| 1 |
| 4 |
当x=5,则
| 1 |
| x |
| 1 |
| 5 |
当x=6,则
| 1 |
| x |
| 1 |
| 6 |
当x=0,则
| 1 |
| x |
即{1},{-1},{2,
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
即和谐集合有25-1=31个,
故选:D.
点评:本题主要考查集合的判断,利用条件确定集合元素之间的关系是解决本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
函数f(x)=sin(x+φ)+cos(x+φ)为奇函数,则φ的一个可能取值( )
| A、0 | ||
B、
| ||
C、-
| ||
D、-
|
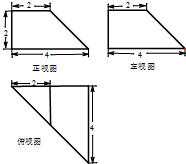 某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )
某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|
若函数f(x+3)的定义域为[-5,-2],则F(x)=f(x+1)+f(x-1)的定义域为( )
| A、[-1,0] |
| B、[-1,1] |
| C、[0,1] |
| D、[-5,-2] |