题目内容
在平行四边形ABCD中，E是DC的中点，AE交BD于点M，|
|=4，|
|=2，
、
的夹角为
．
（1）若
=λ
+μ
，求λ+3μ的值；
（2）当点P在平行四边形ABCD的边BC和CD上运动时，求
•
的取值范围．
| AB |
| AD |
| AB |
| AD |
| π |
| 3 |
（1）若
| AM |
| AC |
| BD |
（2）当点P在平行四边形ABCD的边BC和CD上运动时，求
| AP |
| AE |
考点：平面向量数量积的运算,向量加减混合运算及其几何意义
专题：平面向量及应用
分析：（1）如图所示，由于在平行四边形ABCD中，E是DC的中点，AE交BD于点M，可得
=
，利用三角形法则和共线定理可得
=
+
，可得
=
+
．利用三角形法则可得
，
，分别用
，
表示，代入
=λ
+μ
，比较即可得出．
（2）通过建立直角坐标系，利用共线定理和及时性法则即可得出．
| AM |
| 2 |
| 3 |
| AE |
| AE |
| AD |
| 1 |
| 2 |
| AB |
| AM |
| 2 |
| 3 |
| AD |
| 1 |
| 3 |
| AB |
| AC |
| BD |
| AD |
| AB |
| AM |
| AC |
| BD |
（2）通过建立直角坐标系，利用共线定理和及时性法则即可得出．
解答：
解：（1）如图所示，
∵在平行四边形ABCD中，E是DC的中点，AE交BD于点M，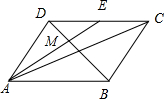
∴
=
，
又
=
+
=
+
=
+
，
∴
=
(
+
)=
+
．
=
+
，
=
-
，
代入
=λ
+μ
，
可得
+
=λ(
+
)+μ(
-
)=(λ+μ)
+(λ-μ)
，
∴
，解得λ=
，μ=
．
∴λ+3μ=
+3×
=1．
（2）如图所示，建立直角坐标系．
则A（0，0），B（4，0），C(5，
)，D(1，
)，E(3，
)．
∴
=（4，0）=
，
=(1，
)=
，
=(3，
)，．
①当点P位于边BC上时，设
=λ
（0≤λ≤1）．
则
=
+
=
+λ
=（4，0）+λ(1，
)=(4+λ，
λ)．
∴
•
=(4+λ，
λ)•(3，
)
=3（4+λ）+3λ
=6λ+12，
∵0≤λ≤1，∴12≤6λ+12≤18．
∴
•
的取值范围是[12，18]．
②当点P位于边CD上时，设
=μ
（0≤μ≤1）．
∴
=
+
=
+μ
=(1，
)+μ(4，0)=(1+4μ，
)．
∴
•
=(1+4μ，
)•(3，
)=3（1+4μ）+3=12μ+6．
∵0≤μ≤1，∴6≤12μ+6≤18．
∴
•
的取值范围是[6，18]．
综上①②可知：
•
的取值范围是[6，18]．
∵在平行四边形ABCD中，E是DC的中点，AE交BD于点M，
∴
| AM |
| 2 |
| 3 |
| AE |
又
| AE |
| AD |
| DE |
| AD |
| 1 |
| 2 |
| DC |
| AD |
| 1 |
| 2 |
| AB |
∴
| AM |
| 2 |
| 3 |
| AD |
| 1 |
| 2 |
| AB |
| 2 |
| 3 |
| AD |
| 1 |
| 3 |
| AB |
| AC |
| AD |
| AB |
| BD |
| AD |
| AB |
代入
| AM |
| AC |
| BD |
可得
| 2 |
| 3 |
| AD |
| 1 |
| 3 |
| AB |
| AD |
| AB |
| AD |
| AB |
| AD |
| AB |
∴
|
| 1 |
| 2 |
| 1 |
| 6 |
∴λ+3μ=
| 1 |
| 2 |
| 1 |
| 6 |
（2）如图所示，建立直角坐标系．
则A（0，0），B（4，0），C(5，
| 3 |
| 3 |
| 3 |
∴
| AB |
| DC |
| BC |
| 3 |
| AD |
| AE |
| 3 |
①当点P位于边BC上时，设
| BP |
| BC |
则
| AP |
| AB |
| BP |
| AB |
| BC |
| 3 |
| 3 |
∴
| AP |
| AE |
| 3 |
| 3 |
=3（4+λ）+3λ
=6λ+12，
∵0≤λ≤1，∴12≤6λ+12≤18．
∴
| AP |
| AE |
②当点P位于边CD上时，设
| DP |
| DC |
∴
| AP |
| AD |
| DP |
| AD |
| DC |
| 3 |
| 3 |
∴
| AP |
| AE |
| 3 |
| 3 |
∵0≤μ≤1，∴6≤12μ+6≤18．
∴
| AP |
| AE |
综上①②可知：
| AP |
| AE |
点评：本题考查了向量的三角形法则、共线定理、线性运算、一次函数的单调性、数量积等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
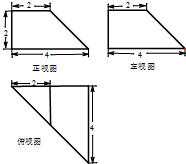某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形．则该几何体的表面积为（ ）A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|