题目内容
设α，β，γ为两两不重合的平面，m，n为两条不重合的直线，给出下列四个命题：
①若α⊥γ，β∥γ，则α⊥β；
②若α∥γ，β∥γ，则α∥β；
③若m∥α，n∥α，则m∥n；
④若α⊥γ，β⊥γ，α∩β=m，则m⊥γ；
其中真命题的个数是（ ）
①若α⊥γ，β∥γ，则α⊥β；
②若α∥γ，β∥γ，则α∥β；
③若m∥α，n∥α，则m∥n；
④若α⊥γ，β⊥γ，α∩β=m，则m⊥γ；
其中真命题的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：命题的真假判断与应用,空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题：空间位置关系与距离
分析：根据直线和平面的位置关系和平面与平面的位置关系对选项加以一一判断，选出正确的命题．
解答：
解：对①，应用面面垂直的性质定理和面面平行的性质可知①对；
对②，由面面平行的传递性可知②也对；
对③，若m∥α，n∥α，则m∥n或m，n相交或异面，故③错；
对④，应用面面垂直的性质定理或联想开门动作，容易得④也对．
所以真命题的个数是3，
故选：C．
对②，由面面平行的传递性可知②也对；
对③，若m∥α，n∥α，则m∥n或m，n相交或异面，故③错；
对④，应用面面垂直的性质定理或联想开门动作，容易得④也对．
所以真命题的个数是3，
故选：C．
点评：本题主要考查平面与平面的位置关系，以及直线与平面的位置关系和直线与直线的位置关系，考查学生的空间想象能力和推理能力，是一道基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
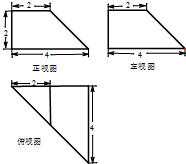某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形．则该几何体的表面积为（ ）A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|
复数
的共轭复数是（ ）
| 1 |
| i |
| A、i | B、-i | C、1 | D、0 |