题目内容
在△ABC中，a、b、c分别为内角A、B、C的对边，且（a2+b2）sin（A-B）=（a2+b2）sin（A+B），则△ABC是（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
考点：余弦定理
专题：解三角形
分析：由条件可得sin（A-B）=sin（A+B），再由 A-B≠A+B，可得A-B+（A+B）=π，故有 A=
，从而得出结论．
| π |
| 2 |
解答：
解：在△ABC中，由（a2+b2）sin（A-B）=（a2+b2）sin（A+B），
可得sin（A-B）=sin（A+B），∵A-B≠A+B，∴A-B+（A+B）=π，∴A=
，
故△ABC是直角三角形，
故选：B．
可得sin（A-B）=sin（A+B），∵A-B≠A+B，∴A-B+（A+B）=π，∴A=
| π |
| 2 |
故△ABC是直角三角形，
故选：B．
点评：本题主要考查诱导公式的应用，得到A-B+（A+B）=π，是解题的关键，属于中档题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
函数f（x）=sin（x+φ）+cos（x+φ）为奇函数，则φ的一个可能取值（ ）
| A、0 | ||
B、
| ||
C、-
| ||
D、-
|
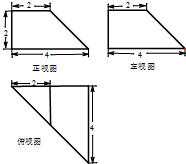某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形．则该几何体的表面积为（ ）A、6+12
| ||
B、16+12
| ||
C、6+12
| ||
D、16+12
|
若函数f（x+3）的定义域为[-5，-2]，则F（x）=f（x+1）+f（x-1）的定义域为（ ）
| A、[-1，0] |
| B、[-1，1] |
| C、[0，1] |
| D、[-5，-2] |