题目内容
已知O为△ABC内一点,满足
+
+
=
.若
+
=λ
,则实数λ= .
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
| AO |
考点:平面向量的基本定理及其意义,向量的共线定理
专题:计算题,平面向量及应用
分析:由题意,可根据向量的线性运算性质,将
+
=λ
转化(λ-2)
+
+
=
.根据向量相等的条件得出λ的方程,解方程求值.
| AB |
| AC |
| AO |
| OA |
| OB |
| OC |
| 0 |
解答:
解:∵
+
=λ
,
∴
-
+
-
+λ
=
,即(λ-2)
+
+
=
.
∴λ-2=1,解得λ=3.
故答案为3.
| AB |
| AC |
| AO |
∴
| OB |
| OA |
| OC |
| OA |
| OA |
| 0 |
| OA |
| OB |
| OC |
| 0 |
∴λ-2=1,解得λ=3.
故答案为3.
点评:本题考查了向量相等的条件,同一性的思想,利用同一性建立所求参数的等式进行求解是一个常用的技巧.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
某小组有3名男生和2名女生,从中任选2名学生参加演讲比赛,那么对立的两个事件( )
| A、至少有1名男生和全是男生 |
| B、至少有1名男生和至少有1名女生 |
| C、恰有1名男生和恰有1名女生 |
| D、至少有1名男生和全是女生 |
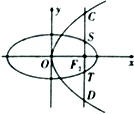 如图,椭圆E:
如图,椭圆E: