题目内容
在△ABC中,点D为BC的中点,若AB=
,AC=3,则
•
=( )
| 5 |
| BC |
| AD |
| A、1 | B、2 | C、3 | D、4 |
考点:平面向量数量积的运算,余弦定理
专题:平面向量及应用
分析:利用三角形中线的性质将
和
分别用
,
表示,然后进行向量的模的运算即可.
| AD |
| BC |
| AB |
| AC |
解答:
解:因为在△ABC中,点D为BC的中点,
所以
=
(
+
),
=
-
,
因为AB=
,AC=3,
所以
•
=
(
+
)(
-
)=
(
2-
2)=
×[32-(
)2]=2;
故选B.
所以
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BC |
| AC |
| AB |
因为AB=
| 5 |
所以
| BC |
| AD |
| 1 |
| 2 |
| AC |
| AB |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 2 |
| 5 |
故选B.
点评:本题考查了向量的三角形法则的运用以及向量的乘法的计算,运用了向量的平方与其模的平方相等使问题得到解决.

练习册系列答案
相关题目
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为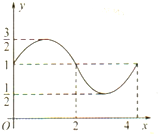 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
到两坐标轴距离相等的点的轨迹方程是( )
| A、y=x |
| B、x2-y2=0 |
| C、y=-x |
| D、y=|x| |
函数y=lnx+x的零点位于区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |