题目内容
点P(3,1)在椭圆
+
=1(a>b>0)的右准线上,过P点的方向向量为
=(-2,-5)的光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| a |
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:根据对称性可知光线经过直线y=-2反射后的直线过已知过点P(3,1)且方向为
=(-2,-5)的直线 与y=-2的交点,反射后所在的直线与x轴的交点即为椭圆的右焦点,从而可求c,再由右准线方程,求得a,再由离心率公式,即可得到.
| a |
解答:
解:由题意可得过点P(3,1)的直线的方程为:y-1=
(x-3),
与y=-2的交点为(
,-2),
光线经过直线y=-2反射后所在的直线方程为y+2=-
(x-
),
与x轴的交点(1,0)即为椭圆的右焦点,即c=1,
由于点P(3,1)在椭圆
+
=1(a>b>0)的右准线上,
则
=3,即a2=3c=3,则离心率为e=
=
.
故答案为:
.
| 5 |
| 2 |
与y=-2的交点为(
| 9 |
| 5 |
光线经过直线y=-2反射后所在的直线方程为y+2=-
| 5 |
| 2 |
| 9 |
| 5 |
与x轴的交点(1,0)即为椭圆的右焦点,即c=1,
由于点P(3,1)在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
则
| a2 |
| c |
| c |
| a |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题主要考查了利用对称性求解直线方程,解题的关键是要发现反射关系过入射关系与y=-2的焦点,还要注意方向向量的概念的理解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设a>0且a≠1,则“函数f(x)=ax在x上是减函数”,是“函数g(x)=(2-a)x3在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
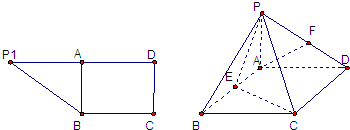
 如图,PA⊥平面ABC,∠ABC=90°且PA=AB=BC=a,则异面直线PB与AC所成角的正切值等于
如图,PA⊥平面ABC,∠ABC=90°且PA=AB=BC=a,则异面直线PB与AC所成角的正切值等于 某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有
某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有