Question

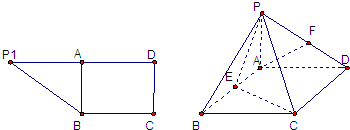
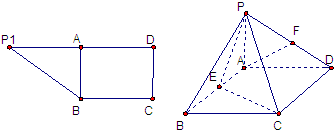
如图，在直角梯形P₁DCB中，P₁D∥BC，CD⊥P₁D且P₁D=6，BC=3，DC=

6

，A是P₁D的中点，沿AB把平面P₁AB折起到平面PAB的位置，使二面角P-CD-B成45°，设E、F分别为线段AB、PD的中点．
（1）求证：AF∥面PEC；
（2）求PC与底面ABCD所成角的正弦值；
（3）求D到面ACF的距离．

Answer 1

考点：点、线、面间的距离计算,直线与平面平行的判定,直线与平面所成的角

专题：空间位置关系与距离,空间角

分析：（1）法一：判断出AF∥EM，又AF?面PEC，EM?面PEC，运用判定定理即可证明．
法二：取CD中点为N，判断得出面AFN∥面PEC，即可证明AF∥面PEC；
（2）判断出∠PCA为PC与底面所成的角，在Rt△PAC中解决即可．
（3）由VD-ACF=VF-ACD得：

1

3

d•S△ACF=

1

3

•

1

2

PA•S△ACD，利用等积法求解即可．

解答： 解：（1）法一：取PC中点为M，
∵E、F分别为AB、PD中点，
∴FM

∥ .

.

1

2

DC∴FM

∥ .

.

AE
则AF∥EM，又AF?面PEC，EM?面PEC，
∴AF∥面PEC．
法二：取CD中点为N，
∵E、F分别为AB、PD中点，则EC∥AN，又FN∥PC，
∴面AFN∥面PEC，
则AF∥面PEC．
（2）∵PA⊥AB，又AB⊥AD，
∴AB⊥PD，
又∵CD∥AB，
∴CD⊥PD，CD⊥AD，
∴∠PDA为二面角P-CD-B的平面角，即∠PDA=45°，
在△PDA中，PD=AD=3，
∴PA⊥AD，则PA⊥面ABCD
从而∠PCA为PC与底面所成的角，
在Rt△PAC中，
PA=3，AC=

32+6

=

15

∴PC=2

6

则sin∠PCA=

PA

PC

=

6

4

（3）设D到面ACF的距离为d，
由VD-ACF=VF-ACD得：

1

3

d•S△ACF=

1

3

•

1

2

PA•S△ACD，
∵PA=AD=3，F为PD中点，
∴AF⊥PD，又CD⊥面PAD，
∴AF⊥CD即AF⊥FC，
在△AFC中，AF=

3 2

2

，AC=

15

∴FC=

15-( 3 2 2 )2

=

42

2

∴S△AFC=

1

2

•AF•FC=

3 21

4

又S△ADC=

1

2

•3•

6

=

3 6

2

，
由

1

3

•d•

3 21

4

=

1

3

•

3

2

•

2 6

2

得d=

3 14

7

，
即D到面ACF的距离为

3 14

7

．

点评：本题综合考查了空间点线面的距离问题，线面的位置关系判断，属于中档题．