Question

如图，PA⊥平面ABC，∠ABC=90°且PA=AB=BC=a，则异面直线PB与AC所成角的正切值等于

 

．

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：作图，分别取PA、AB、BC的中点D、E、F，连结DE、DF、EF、AF，则DE‖PB，EF‖AC，所以∠DEF或其补角即为所求，由PA=AB=BC=a，利用勾股定理及余弦定理即可求得cos∠DEF，从而求得异面直线PB与AC所成角的正切值．

解答： 解：如图所示：分别取PA、AB、BC的中点D、E、F，连结DE、DF、EF、AF，

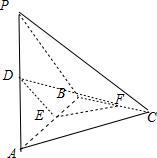
则DE‖PB，EF‖AC，所以∠DEF或其补角即为所求，
∵PA=AB=BC=a，PA⊥平面ABC，∠ABC=90°，
∴△PAB，△ABC均为Rt△，
所以DE=EF=

2

2

a，DF=

DA2+AF2

=

DA2+AB2+BF2

=

6

2

a，
根据c²=a²+b²-2abcosC可得cos∠DEF=

1

2

，
所以∠DEF=

π

3

，
所以tan∠DEF=

3

，
所以PB与AC的夹角的正切值为

3

．
故答案为：

3

；

点评：本题考查线面垂直的性质及异面角的求解，异面角的常用求解方法有：①平移法：通过平移直线把空间角转化为平面角求解，其步骤为：一作、二证、三求；②向量法：转化为相应直线的方向向量的夹角求解；注意异面角的范围：（0，

π

2

]．