题目内容
某城市的交通道路如图，从城市的东南角A到城市的西北角B，不经过十字道路维修处C，最近的走法种数有考点：排列、组合及简单计数问题
专题：排列组合
分析：先求出从城市的东南角A到城市的西北角B，最近的走法种数，然后求出从城市的东南角A到城市的西北角B，经过十字道路维修处C，最近的走法种数，即可求出从城市的东南角A到城市的西北角B，不经过十字道路维修处C，最近的走法种数．
解答：
解：从城市的东南角A到城市的西北角B，最近的走法种数共有：C94=126种走法．
从城市的东南角A经过十字道路维修处C，最近的走法有C52=10，从C到城市的西北角B，最近的走法种数C42=6，
所以从城市的东南角A到城市的西北角B，经过十字道路维修处C，最近的走法种数：10×6=60．
所以从城市的东南角A到城市的西北角B，不经过十字道路维修处C，
最近的走法种数有：126-60=66．
故答案为：66
从城市的东南角A经过十字道路维修处C，最近的走法有C52=10，从C到城市的西北角B，最近的走法种数C42=6，
所以从城市的东南角A到城市的西北角B，经过十字道路维修处C，最近的走法种数：10×6=60．
所以从城市的东南角A到城市的西北角B，不经过十字道路维修处C，
最近的走法种数有：126-60=66．
故答案为：66
点评：本题考查排列组合以及简单的计数原理的应用，采用逆向思维是解决本题的关键，属于中档题，
练习册系列答案
相关题目
已知t＞0，若
（2x-2）dx=3，则t=（ ）
| ∫ | t 0 |
| A、3 | B、2 | C、1 | D、3或-1 |
已知f（x）=
，则下列结论成立的是（ ）
|
| A、f（x）在x=0处连续 | ||
B、
| ||
C、
| ||
D、
|
设a，b，c表示三条不同直线，α，β表示两个不同平面，则下列命题中逆命题不成立的是（ ）
| A、b?β，c是α在β内的射影，若b⊥c，则b⊥a |
| B、b?α，c?α，若c∥α，则b∥c |
| C、c⊥α，若c⊥β，则α∥β |
| D、b?β，若b⊥α，则β⊥α |
如图所示，在边长为2的正方形中有一封闭曲线围成的阴影区域．在正方形中随机撒一粒豆子，它落在阴影区域内的概率为若＜
，
＞=60°，|
|=4，(
+2
)•(
-3
)=-72，则|
|=（ ）
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| A、2 | B、4 | C、6 | D、12 |
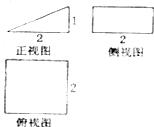
锐角△ABC的内心为I，过点A作直线BI的垂线，垂足为H，点E为内切圆I与边CA的切点．若∠C=50°，则∠IEH的度数=一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|