题目内容
已知关于x,y的二元二次方程x2+y2+2x-4y+k=0(k∈R)表示圆C.
(1)求圆心C的坐标;
(2)求实数k的取值范围;
(3)是否存在实数k,使直线l:x-2y+4=0与圆C相交于M、N两点,且OM⊥ON(O为坐标原点)?若存在,请求出k的值,若不存在,说明理由.
(1)求圆心C的坐标;
(2)求实数k的取值范围;
(3)是否存在实数k,使直线l:x-2y+4=0与圆C相交于M、N两点,且OM⊥ON(O为坐标原点)?若存在,请求出k的值,若不存在,说明理由.
考点:直线和圆的方程的应用,二元二次方程表示圆的条件
专题:综合题,直线与圆
分析:(1)由方程x2+y2+2x-4y+k=变形为(x+1)2+(y-2)2=5-k,可得圆心C的坐标;
(2)由于此方程表示圆,可得5-k>0,解出即可;
(3)设M(x1,y1),N(x2,y2).与圆的方程联立可得△>0及根与系数关系,再利用OM⊥ON,可得x1x2+y1y2=5y1y2-8(y1+y2)+16=0,即可解出k.
(2)由于此方程表示圆,可得5-k>0,解出即可;
(3)设M(x1,y1),N(x2,y2).与圆的方程联立可得△>0及根与系数关系,再利用OM⊥ON,可得x1x2+y1y2=5y1y2-8(y1+y2)+16=0,即可解出k.
解答:
解:(1)由方程x2+y2+2x-4y+k=变形为(x+1)2+(y-2)2=5-k.
∴圆心C的坐标为(-1,2);
(2)∵此方程表示圆,∴5-k>0,解得k<5,故k的取值范围是(-∞,5);
(3)设M(x1,y1),N(x2,y2).
联立直线与圆可得5y2-16y+8+k=0,
∵直线与圆相交,∴△=162-20(8+k)>0,化为k<
.
∴y1+y2=
,y1y2=
.
∴x1x2=(4-2y1)(4-2y2)=16-8(y1+y2)+4y1y2,
∵OM⊥ON,
∴x1x2+y1y2=5y1y2-8(y1+y2)+16=0,
∴8+k-
+16=0,
解得k=
,满足k<
,
故k=
.
∴圆心C的坐标为(-1,2);
(2)∵此方程表示圆,∴5-k>0,解得k<5,故k的取值范围是(-∞,5);
(3)设M(x1,y1),N(x2,y2).
联立直线与圆可得5y2-16y+8+k=0,
∵直线与圆相交,∴△=162-20(8+k)>0,化为k<
| 24 |
| 5 |
∴y1+y2=
| 16 |
| 5 |
| 8+m |
| 5 |
∴x1x2=(4-2y1)(4-2y2)=16-8(y1+y2)+4y1y2,
∵OM⊥ON,
∴x1x2+y1y2=5y1y2-8(y1+y2)+16=0,
∴8+k-
| 8×16 |
| 5 |
解得k=
| 8 |
| 5 |
| 24 |
| 5 |
故k=
| 8 |
| 5 |
点评:本题考查了直线与圆相交问题转化为方程联立得到△>0及根与系数关系、向量垂直与数量积的关系等基础知识与基本技能方法,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为( )
| A、27π | B、9π | C、3π | D、π |
一个几何体的三视图如图所示,则这个几何体的表面积为( )
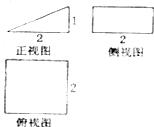

A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|
由
>
,
>
,
>
若a>b>0,m>0,则
与
的关系( )
| 7 |
| 10 |
| 5 |
| 8 |
| 9 |
| 11 |
| 8 |
| 10 |
| 21 |
| 25 |
| 15 |
| 19 |
| b+m |
| a+m |
| b |
| a |
| A、相等 | B、前者大 |
| C、后者大 | D、不确定 |
已知函数f(x)=3cos(x+
)
(1)写出函数f(x)的周期;
(2)将函数f(x)图象上所有的点向右平移
个单位,得到函数g(x)的图象,写出函数g(x)的表达式,并判断函数g(x)的奇偶性.
| π |
| 6 |
(1)写出函数f(x)的周期;
(2)将函数f(x)图象上所有的点向右平移
| π |
| 6 |
已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为4
,则直线l的方程为( )
| 5 |
| A、2x-y+3=0 |
| B、x+2y+9=0 |
| C、x-2y-9=0 |
| D、2x-y+3=0或x+2y+9=0 |