题目内容
在平面直角坐标系中,原点O在以A,B为直径的圆C外,O点到⊙C的切线长为l;
(Ⅰ)证明:l2=
•
;
(Ⅱ)若点A在抛物线y=x2+1上,点B在圆x2+(y-3)2=1,求l的最小值.
(Ⅰ)证明:l2=
| OA |
| OB |
(Ⅱ)若点A在抛物线y=x2+1上,点B在圆x2+(y-3)2=1,求l的最小值.
考点:圆与圆锥曲线的综合
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设A(x1,y1),B(x2,y2),求出C,l2=OC2-(
)2化简即可证明结论.
(Ⅱ)若点A在抛物线y=x2+1上,点B在圆x2+(y-3)2=1,利用(Ⅰ)求出l的表达式,利用不等式化简,构造函数,通过函数的导数求出最小值.
| AB |
| 2 |
(Ⅱ)若点A在抛物线y=x2+1上,点B在圆x2+(y-3)2=1,利用(Ⅰ)求出l的表达式,利用不等式化简,构造函数,通过函数的导数求出最小值.
解答:
解:(Ⅰ)证明:设A(x1,y1),B(x2,y2),则C(
,
),…(2分)
l2=OC2-(
)2=(
)2+(
)2-
[(x1-x2)2+(y1-y2)2]…(4分)
∴l2=x1x2+y1y2=
•
…(6分)
(Ⅱ)依题意y1=x12+1,x22+(y2-3)2=1
∴l2=x1x2+y1y2=x1x2+(x12+1)y2=y2(x1+
)2+y2-
…(8分)
≥y2-
=
+
-
(2≤y2≤4)…(10分)
设h(t)=
+
(2≤t≤4),
则h′(t)=
-
>0(2≤t≤4)
∴h(t)=
+
在[2,4]是增函数;
∴h(t)min=h(2)=
…(12分)
∴lmin=
…(13分)
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
l2=OC2-(
| AB |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 4 |
∴l2=x1x2+y1y2=
| OA |
| OB |
(Ⅱ)依题意y1=x12+1,x22+(y2-3)2=1
∴l2=x1x2+y1y2=x1x2+(x12+1)y2=y2(x1+
| x2 |
| 2y2 |
| x22 |
| 4y2 |
≥y2-
| 1-(y2-3)2 |
| 4y2 |
| 5y2 |
| 4 |
| 2 |
| y 2 |
| 3 |
| 2 |
设h(t)=
| 5t |
| 4 |
| 2 |
| t |
则h′(t)=
| 5 |
| 4 |
| 2 |
| t2 |
∴h(t)=
| 5t |
| 4 |
| 2 |
| t |
∴h(t)min=h(2)=
| 7 |
| 2 |
∴lmin=
| 2 |
点评:本题考查圆与圆锥曲线的综合应用,函数的导数的应用,综合性比较强,考查分析问题解决问题的能力.

练习册系列答案
相关题目
已知函数f(x)=
若f(x)=2,则x的值为( )
|
| A、log32 |
| B、log23 |
| C、32 |
| D、2 |
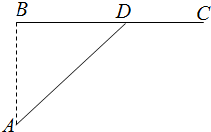 如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ