题目内容
已知三棱锥的底面是边长为
的等边三角形,侧棱长都为2,则侧棱与底面所成角的大小为( )
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
考点:棱锥的结构特征
专题:计算题,空间位置关系与距离
分析:结合图形,过顶点作底面的垂线,根据线面角的定义可得侧棱与底面所成的角,再根据正棱锥的结构特征求相关几何量的数据,解三角形求角.
解答:
解:作SO⊥平面ABC,则O为正三角形ABC的中心,
∴∠SAO为侧棱SA与底面ABC所成的角,
OA=
×AD=
×
×
=1,SA=2,
在Rt△SAO中,cos∠SAO=
,
∴∠SAO=60°.
故选:C.

∴∠SAO为侧棱SA与底面ABC所成的角,
OA=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
在Rt△SAO中,cos∠SAO=
| 1 |
| 2 |
∴∠SAO=60°.
故选:C.

点评:本题考查了正三棱锥的结构特征及直线与平面所成角的求法,熟练掌握线面角的定义及正棱锥的结构特征是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
二次不等式ax2+bx+1>0的解集为{x|-1<x<
},则ab的值为( )
| 1 |
| 3 |
| A、-5 | B、5 | C、-6 | D、6 |
已知圆x2-x+y2=6经过双曲线
-
=1(a,b>0)的左顶点和右焦点,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
双曲线
-
=1的左、右焦点为F1,F2,直线x=
与双曲线的渐近线交于点P,过点P且与x轴平行的直线交双曲线右支于点M,过点M做x轴的垂线,垂足为N,若
=3
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 2 |
| F1N |
| NF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直线mx+(1-n)y+1=0(m>0,n>0)和直线x+2y+1=0平行,则
+
的最小值是( )
| 1 |
| m |
| 1 |
| n |
A、2
| ||
B、3+2
| ||
C、4
| ||
D、3+
|
函数f(x)=xsinx在区间[0,4]上的零点个数( )
| A、0 | B、1 | C、2 | D、3 |
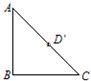 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )