题目内容
已知直线mx+(1-n)y+1=0(m>0,n>0)和直线x+2y+1=0平行,则
+
的最小值是( )
| 1 |
| m |
| 1 |
| n |
A、2
| ||
B、3+2
| ||
C、4
| ||
D、3+
|
考点:基本不等式
专题:不等式的解法及应用
分析:由两直线平行,斜率相等列出方程,解方程求得m值.再把
+
化为(2m+n)(
+
),根据基本不等式求解即可.
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
解答:
解:∵直线mx+(1-n)y+1=0(m>0,n>0)和直线x+2y+1=0平行,
∴它们的斜率相等,即
=-
,
∴2m+n=1,
∴
+
=(2m+n)(
+
)=3+
+
≥3+2
=3+2
∴
+
的最小值是3+2
故选:B.
∴它们的斜率相等,即
| m |
| n-1 |
| 1 |
| 2 |
∴2m+n=1,
∴
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
| 2m |
| n |
| n |
| m |
|
| 2 |
∴
| 1 |
| m |
| 1 |
| n |
| 2 |
故选:B.
点评:本题考查两直线平行的性质以及基本不等式的应用,考查了灵活运用知识的能力.

练习册系列答案
相关题目
已知三棱锥的底面是边长为
的等边三角形,侧棱长都为2,则侧棱与底面所成角的大小为( )
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
在数列{an}中,a1=1,a2=
,且
+
=
(n≥3,n∈N*),则a4=( )
| 2 |
| 3 |
| 1 |
| an-2 |
| 1 |
| an |
| 2 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
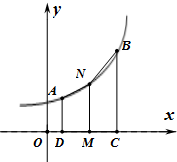
 函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )
函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )A、[
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
设函数f(x)=x2-2ax+b(a,b∈R),则“f(x)=0在区间[1,2]有两个不同的实根”是“1<a<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 已知函数f(x)=lnx.
已知函数f(x)=lnx.