题目内容
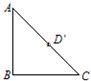将一个边长为2的正方形ABCD沿其对角线AC折起，其俯视图如图所示，此时连接顶点B，D形成三棱锥B-ACD，则其正（主）视图的面积为（ ）| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：根据原来的正方形和俯视图可知，平面ABC与平面ACD垂直，三棱锥B-ACD正视图为底边套2，高为
的三角形，代入三角形面积公式，可得答案．
| 2 |
解答：
解：解：由正视图和俯视图可知，
平面ABC⊥平面ACD．
三棱锥B-ACD的正视图为底边套2，高为
的三角形，
故S=
×2×
=
，
故选：C
平面ABC⊥平面ACD．
三棱锥B-ACD的正视图为底边套2，高为
| 2 |
故S=
| 1 |
| 2 |
| 2 |
| 2 |
故选：C
点评：本题考查简单空间图形的三视图，考查根据原图与另外的三视图，确定第三个三视图的形状，本题是一个基础题．
练习册系列答案
阅读快车系列答案
相关题目
给出如下四个命题：
①若“p∨q”为真命题，则p、q均为真命题；
②“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”；
③“?x∈R，x2+x≥1”的否定是“?x0∈R，x02+x0≤1”；
④“x＞0”是“x+
≥2”的充要条件．
其中不正确的命题是（ ）
①若“p∨q”为真命题，则p、q均为真命题；
②“若a＞b，则2a＞2b-1”的否命题为“若a≤b，则2a≤2b-1”；
③“?x∈R，x2+x≥1”的否定是“?x0∈R，x02+x0≤1”；
④“x＞0”是“x+
| 1 |
| x |
其中不正确的命题是（ ）
| A、①② | B、②③ | C、①③ | D、③④ |
对于直线m、n和平面α、β、γ，有如下五个命题：
①若m∥α，m⊥n，则n⊥α；
②若m⊥α，m⊥n，则n∥α；
③若α⊥β，γ⊥β，则α∥γ；
④若m⊥α，m∥n，n?β，则α⊥β；
⑤若α∩β=m，β∩γ=n，m∥n，则α∥γ；
其中正确的命题个数为（ ）
①若m∥α，m⊥n，则n⊥α；
②若m⊥α，m⊥n，则n∥α；
③若α⊥β，γ⊥β，则α∥γ；
④若m⊥α，m∥n，n?β，则α⊥β；
⑤若α∩β=m，β∩γ=n，m∥n，则α∥γ；
其中正确的命题个数为（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
已知三棱锥的底面是边长为
的等边三角形，侧棱长都为2，则侧棱与底面所成角的大小为（ ）
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |