题目内容
已知曲线C1的极坐标方程为ρ=4cosθ,C2的极坐标方程为ρsin(θ+
)=
,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l经过C2与x轴的交点;
(1)求C1的参数方程,并写出直线l的一个参数方程;
(2)若直线l与C1交于A,B两点,|AB|≤
,求直线l的倾斜角的取值范围.
| π |
| 4 |
| ||
| 2 |
(1)求C1的参数方程,并写出直线l的一个参数方程;
(2)若直线l与C1交于A,B两点,|AB|≤
| 14 |
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)曲线C1的极坐标方程,化为直角坐标,再求C1的参数方程,求出C2的直角坐标,可得直线l经过C2与x轴的交点,从而写出直线l的一个参数方程;
(2)设直线l:y=k(x-1),即kx-y-k=0,直线l与C1交于A,B两点,|AB|≤
,可得圆心到直线的距离≥
=
,从而
≥
,求出k的范围,即可求直线l的倾斜角的取值范围.
(2)设直线l:y=k(x-1),即kx-y-k=0,直线l与C1交于A,B两点,|AB|≤
| 14 |
22-(
|
| ||
| 2 |
| |k| | ||
|
| ||
| 2 |
解答:
解:(1)曲线C1的极坐标方程为ρ=4cosθ,可化为ρ2=4ρcosθ,即x2+y2=4x,
即(x-2)2+y2=4,
∴C1的参数方程为
(α为参数);
C2的极坐标方程为ρsin(θ+
)=
,可化为x+y-1=0,
令y=0,可得x=1,∴直线l的一个参数方程为
(θ为参数);
(2)设直线l:y=k(x-1),即kx-y-k=0,则
∵直线l与C1交于A,B两点,|AB|≤
,
∴圆心到直线的距离≥
=
,
∴
≥
,
∴k2≥1,
∴k≤-1或k≥1,
又k不存在时也满足题意,
∴直线l的倾斜角的取值范围为[
,
].
即(x-2)2+y2=4,
∴C1的参数方程为
|
C2的极坐标方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
令y=0,可得x=1,∴直线l的一个参数方程为
|
(2)设直线l:y=k(x-1),即kx-y-k=0,则
∵直线l与C1交于A,B两点,|AB|≤
| 14 |
∴圆心到直线的距离≥
22-(
|
| ||
| 2 |
∴
| |k| | ||
|
| ||
| 2 |
∴k2≥1,
∴k≤-1或k≥1,
又k不存在时也满足题意,
∴直线l的倾斜角的取值范围为[
| π |
| 4 |
| 3π |
| 4 |
点评:本题考查极坐标方程、参数方程、直角坐标方程之间的互化、应用.考查了直线、圆的基本知识,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知三棱锥的底面是边长为
的等边三角形,侧棱长都为2,则侧棱与底面所成角的大小为( )
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
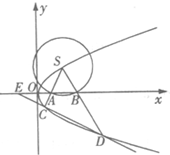 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<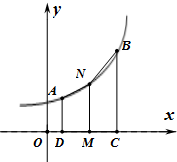 已知函数f(x)=lnx.
已知函数f(x)=lnx.