题目内容
已知正三棱锥P-ABC的主视图和俯视图如图所示，则此三棱锥的外接球的表面积为 ．
考点：球的体积和表面积,球内接多面体
专题：空间位置关系与距离
分析：根据三视图判断正三棱锥的侧棱长与底面正三角形的边长，借助直观图求出外接球的半径，代入球的表面积公式计算．
解答：
解：由正视图与侧视图知，正三棱锥的侧棱长为4，底面正三角形的边长为2
，如图：
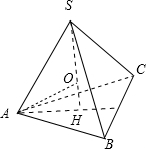
其中SA=4，AH=
×2
×
=2，SH=
=2
，
设其外接球的球心为0，半径为R，则：OS=OA=R，
∴R+
=2
⇒R=
，
∴外接球的表面积S=4π×
=
．
故答案为：
| 3 |
其中SA=4，AH=
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 16-4 |
| 3 |
设其外接球的球心为0，半径为R，则：OS=OA=R，
∴R+
| R2-4 |
| 3 |
4
| ||
| 3 |
∴外接球的表面积S=4π×
| 16 |
| 3 |
| 64π |
| 3 |
故答案为：
| 64π |
| 3 |
点评：本题考查了由三视图求几何体的外接球的表面积，根据三棱锥的结构特征求出外接球的半径是解答本题的关键．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
设
如图，A（1，0），B（-
某校在期中考试后，统计了8位同学的考试成绩为如图所示的茎叶图，ai（i=1，2，…，8）是第i名同学的考试成绩，一部分计算见如图所示的程序框图（期中