题目内容
已知数列{an}满足a1=49，an+1=an+2n，则
的最小值为 ．
| an |
| n |
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由数列递推式利用累加法求出数列{an}的通项公式，代入
后由基本不等式求最值．
| an |
| n |
解答：
解：由an+1=an+2n，得
a2-a1=2×1．
a3-a2=2×2．
a4-a3=2×3．
…
an-an-1=2（n-1）（n≥2）．
累加得：an=a1+2（1+2+…+n-1），
∴an=49+2•
=n2-n+49（n≥2）．
验证n=1时上式成立．
∴an=n2-n+49．
则
=
=n+
-1≥2
-1=13．
当且仅当n=
，即n=7时取最小值．
故答案为：13．
a2-a1=2×1．
a3-a2=2×2．
a4-a3=2×3．
…
an-an-1=2（n-1）（n≥2）．
累加得：an=a1+2（1+2+…+n-1），
∴an=49+2•
| n(n-1) |
| 2 |
验证n=1时上式成立．
∴an=n2-n+49．
则
| an |
| n |
| n2-n+49 |
| n |
| 49 |
| n |
n•
|
当且仅当n=
| 49 |
| n |
故答案为：13．
点评：本题考查了数列递推式，训练了累加法求数列的通项公式，训练了利用基本不等式求最值，是中档题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
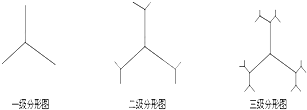某种平面分形图如图所示，一级分形图是由一点出发的三条线段，长度均为1，两两夹角为120°；二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来a＞1，对任意的x∈[a，2a]都有y∈[a，a2]满足方程logax+logay=3，则a的集合（ ）
| A、[2，3] |
| B、[2，+∞） |
| C、（1.25，1.75） |
| D、（1.75，2） |