题目内容
设| e1 |
| e2 |
（1）已知
| AB |
| e1 |
| e2 |
| CB |
| e1 |
| e2 |
| CD |
| e1 |
| e2 |
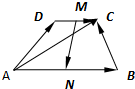
（2）如图，ABCD是一个梯形，
| AB |
| CD |
| AB |
| CD |
| AB |
| e1 |
| AD |
| e2 |
| e1 |
| e2 |
| AC |
| MN |
考点：平行向量与共线向量
专题：平面向量及应用
分析：（1）由已知得
=
-
=
-4
，
，
共线，由此能求出k．
（2）由已知得
=
+
=
+
，
=
+
+
=
-
，由此能求出结果．
| BD |
| CD |
| CB |
| e1 |
| e2 |
| AB |
| BD |
（2）由已知得
| AC |
| AD |
| DC |
| 1 |
| 2 |
| e1 |
| e2 |
| MN |
| MD |
| DA |
| 1 |
| 2 |
| AB |
| 1 |
| 4 |
| AB |
| AD |
解答：
解：（1）
=
-
=（2
-
）（
+3
）=
-4
，…（2分）
∵A，B，C三点共线，∴
，
共线，
∴存在λ使
=λ
，即2
+k
=λ(
-4
)，…（4分）
∴
，解得k=-8．…（6分）
（2）∵
，
是两个不共线的向量，
∴
=
+
=
+
…（8分）
=
+
+
=
-
，
∴
=
-
．…（12分）
| BD |
| CD |
| CB |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∵A，B，C三点共线，∴
| AB |
| BD |
∴存在λ使
| AB |
| BD |
| e1 |
| e2 |
| e1 |
| e2 |
∴
|
（2）∵
| e1 |
| e2 |
∴
| AC |
| AD |
| DC |
| 1 |
| 2 |
| e1 |
| e2 |
| MN |
| MD |
| DA |
| 1 |
| 2 |
| AB |
| 1 |
| 4 |
| AB |
| AD |
∴
| MN |
| 1 |
| 4 |
| e1 |
| e2 |
点评：本题考查实数值的求法，考查向量的表示，是基础题，解题时要注意平面向量加法定理的合理运用．
练习册系列答案
相关题目
函数y=2x3-2x2在[-1，2]上的最大值，最小值为（ ）
| A、0、-3 | B、8、-3 |
| C、10、8 | D、8、-4 |
如图，直三棱柱ABC-A1B1C1中，已知∠ACB=90°，AC=BC=1，BB1=2，M，N分别是B1C1和AB的中点．
如图所示的几何体中，ABCD-A1B1C1D1是一个长方体，P-ABCD是一个四棱锥，其中AB=2，BC=3，AA1=2，点P∈平面CC1D1D且PD=PC=
如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAB是正三角形，AB=2，BC=