题目内容
 如图,A(1,0),B(-
如图,A(1,0),B(-| 1 |
| 2 |
| ||
| 2 |
| 2π |
| 3 |
| OC |
| OA |
| OB |
(1)当α=
| π |
| 3 |
(2)用α表示2λ-μ,并求2λ-μ的取值范围;
(3)当α在区间[0,
| 2π |
| 3 |
考点:平面向量数量积的运算,函数最值的应用,平面向量的基本定理及其意义,平面向量的综合题
专题:平面向量及应用
分析:(1)当α=
时,
=(
,
)=λ
+μ
=(λ-
,
μ),可得λ-
=
,且μ=1,解得 λ 和μ 的值,可得 λ+μ 的值.
(2)由于
=(cosα,sinα)=λ
+μ
,解得λ=cosα+
sinα,μ=
sinα,可得2λ-μ=2cosα,从而得到2λ-μ的范围.
(3)当α在区间[0,
]变化时,由于 μ2+m(2λ-μ)=-
(cosα-
)2+
m2+
的最大值为1,-
≤cosα≤1,再分
<-
、
∈[-
,1]、
>1三种情况,分别根据μ2+m(2λ-μ)的最大值为1,求得实数m的值.
| π |
| 3 |
| OC |
| 1 |
| 2 |
| ||
| 2 |
| OA |
| OB |
| μ |
| 2 |
| ||
| 2 |
| μ |
| 2 |
| 1 |
| 2 |
(2)由于
| OC |
| OA |
| OB |
| ||
| 3 |
2
| ||
| 3 |
(3)当α在区间[0,
| 2π |
| 3 |
| 4 |
| 3 |
| 3m |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 2 |
| 3m |
| 4 |
| 1 |
| 2 |
| 3m |
| 4 |
| 1 |
| 2 |
| 3m |
| 4 |
解答:
解:(1)当α=
时,
=(
,
)=λ
+μ
=λ(1,0)+μ(-
,
)=(λ-
,
μ),
∴λ-
=
,且μ=1,解得 λ=μ=1,∴λ+μ=2.
(2)由于
=(cosα,sinα)=λ
+μ
=λ(1,0)+μ(-
,
)=(λ-
,
μ),
∴cosα=λ-
,sinα=
μ,解得λ=cosα+
sinα,μ=
sinα,
∴2λ-μ=2cosα,显然,2λ-μ∈[-2,2].
(3)当α在区间[0,
]变化时,由于 μ2+m(2λ-μ)=
sin2α+2mcosα=
-
cos2α+2mcosα=-
(cosα-
)2+
m2+
的最大值为1,-
≤cosα≤1,
当
<-
时,即m<-
时,由-
(-
-
)2+
m2+
=1,求得m=0(舍去).
当
∈[-
,1]时,即
≥m≥-
时,由
m2+
=1,求得m无解.
当
>1时,即m>
时,由-
(1-
)2+
m2+
=1,求得m=
(舍去).
故实数m的值不存在.
| π |
| 3 |
| OC |
| 1 |
| 2 |
| ||
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| ||
| 2 |
| μ |
| 2 |
| ||
| 2 |
∴λ-
| μ |
| 2 |
| 1 |
| 2 |
(2)由于
| OC |
| OA |
| OB |
| 1 |
| 2 |
| ||
| 2 |
| μ |
| 2 |
| ||
| 2 |
∴cosα=λ-
| μ |
| 2 |
| ||
| 2 |
| ||
| 3 |
2
| ||
| 3 |
∴2λ-μ=2cosα,显然,2λ-μ∈[-2,2].
(3)当α在区间[0,
| 2π |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3m |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 2 |
当
| 3m |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 3m |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
当
| 3m |
| 4 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 3 |
当
| 3m |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3m |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 2 |
故实数m的值不存在.
点评:本题主要考查两个向量的数量积公式,两个向量坐标形式的运算,二次函数的性质,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
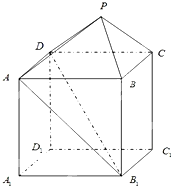 如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=
如图所示的几何体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥,其中AB=2,BC=3,AA1=2,点P∈平面CC1D1D且PD=PC=