题目内容
1.在△ABC中,角A、B、C所对的边分别为a、b、c,且b(2sinB-sinA)+(2a-b)sinA=2csinC,则C=( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根据题意,由正弦定理可以将b(2sinB-sinA)+(2a-b)sinA=2csinC转化为b(2b-a)+(2a-b)a=2c2,变形可得:b2+a2-c2=ab,进而由余弦定理cosC=$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$计算可得cosC的值,由C的范围即可得答案.
解答 解:根据题意,由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$,
又由b(2sinB-sinA)+(2a-b)sinA=2csinC,
有b(2b-a)+(2a-b)a=2c2,
变形可得:b2+a2-c2=ab,
则cosC=$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
则C=$\frac{π}{3}$;
故选:B.
点评 本题考查正弦、余弦定理的运用,关键是利用正弦定理得到三边的关系.

练习册系列答案
相关题目
12.“z1与z2互为共轭复数”是“z1z2∈R”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
9.已知集合U=R(R是实数集),A={x|-1≤x≤1},B={x|x2-2x<0},则A∪(∁UB)=( )
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
6.在△ABC中,若B=2A,$a:b=1:\sqrt{3}$,则A=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
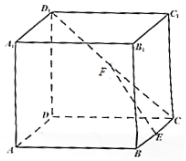 如图,在正方体ABCD-A1B1C1D1中,E、F分别是线段BC、CD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是线段BC、CD1的中点.