题目内容
9．已知集合U=R（R是实数集），A={x|-1≤x≤1}，B={x|x2-2x＜0}，则A∪（∁UB）=（ ）| A． | [-1，0] | B． | [1，2] | C． | [0，1] | D． | （-∞，1]∪[2，+∞） |
分析 解不等式求出集合B，根据补集与并集的定义计算即可．
解答 解：集合U=R（R是实数集），
A={x|-1≤x≤1}，
B={x|x2-2x＜0}={x|0＜x＜2}，
∴∁UB={x|x≤0或x≥2}；
∴A∪（∁UB）={x|x≤1或x≥2}
=（-∞，1]∪[2，+∞）．
故选：D．
点评 本题考查了解不等式以及补集与并集的定义和计算问题，是基础题．
练习册系列答案
相关题目
20．
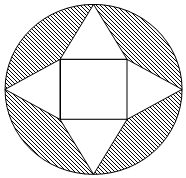如图所示，从一个半径（1+$\sqrt{3}$）m的圆形纸板中切割出一块中间是正方形，四周是四个正三角形的纸板，以此为表面（舍弃阴影部分）折叠成一个正四棱锥，则该四棱锥的体积是（ ）m3．
如图所示，从一个半径（1+$\sqrt{3}$）m的圆形纸板中切割出一块中间是正方形，四周是四个正三角形的纸板，以此为表面（舍弃阴影部分）折叠成一个正四棱锥，则该四棱锥的体积是（ ）m3．| A． | $\frac{4\sqrt{2}}{3}$ | B． | $\frac{2\sqrt{2}}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{\sqrt{2}}{6}$ |
14．已知F1，F2是双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过点F1的直线l与E的左支交于P，Q两点，若|PF1|=2|F1Q|，且F2Q⊥PQ，则E的离心率是（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{7}}{2}$ | C． | $\frac{\sqrt{15}}{3}$ | D． | $\frac{\sqrt{17}}{3}$ |
1．在△ABC中，角A、B、C所对的边分别为a、b、c，且b（2sinB-sinA）+（2a-b）sinA=2csinC，则C=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
如图，四棱锥P-ABCD，侧面PAD是边长为4的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．