题目内容
6．在△ABC中，若B=2A，$a：b=1：\sqrt{3}$，则A=（ ）| A． | 30° | B． | 60° | C． | 90° | D． | 120° |
分析 根据正弦定理，由a与b的比值求出sinA与sinB的比值，然后把B=2A代入，利用二倍角的正弦函数公式化简，再由sinA不为0，在等式两边同时除以sinA，得到cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数．
解答 解：根据正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$得：sinA：sinB=a：b=1：$\sqrt{3}$，
所以sinB=$\sqrt{3}$sinA，又B=2A，
所以sin2A=$\sqrt{3}$sinA，即2sinAcosA=$\sqrt{3}$sinA，
又A为三角形的内角，得到sinA≠0，
所以cosA=$\frac{\sqrt{3}}{2}$，
则A=30°．
故选：A．
点评 此题考查了正弦定理，二倍角的正弦函数公式，以及特殊角的三角函数值，其中根据正弦定理找出边角间的关系，从而利用三角函数的恒等变形得出cosA的值是解本题的关键，属于基础题．
练习册系列答案
期末集结号系列答案
相关题目
16．当$x=\frac{π}{4}$时，函数f（x）=sin（ωx+φ）（A＞0）取得最小值，则函数$y=f（{\frac{3π}{4}-x}）$是（ ）
| A． | 奇函数且图象关于点$（{\frac{π}{2}，0}）$对称 | B． | 偶函数且图象关于点（π，0）对称 | ||
| C． | 奇函数且图象关于直线$x=\frac{π}{2}$对称 | D． | 偶函数且图象关于点$（{\frac{π}{2}，0}）$对称 |
14．已知F1，F2是双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过点F1的直线l与E的左支交于P，Q两点，若|PF1|=2|F1Q|，且F2Q⊥PQ，则E的离心率是（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{7}}{2}$ | C． | $\frac{\sqrt{15}}{3}$ | D． | $\frac{\sqrt{17}}{3}$ |
1．在△ABC中，角A、B、C所对的边分别为a、b、c，且b（2sinB-sinA）+（2a-b）sinA=2csinC，则C=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
3．若函数f（x）=lnx-ax+1，a∈R有两个零点，则实数a的取值范围是（ ）
| A． | （-∞，1） | B． | （0，1） | C． | （-1，1） | D． | （1，2） |
如图，四棱锥P-ABCD，侧面PAD是边长为4的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．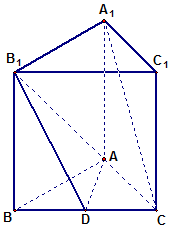
如图，在直三棱柱（侧棱与底面垂直的三棱柱）ABC-A1B1C1中，BB1=8，AB=8，AC=6，BC=10，D是BC边的中点．