题目内容
2.已知实数x,y满足$\left\{\begin{array}{l}{y≥\frac{1}{2}x}\\{x≤7}\\{2x-y≥4}\end{array}\right.$,若z=ax+y有最大值7,则实数a的值为-$\frac{3}{7}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).
则A(7,10),
由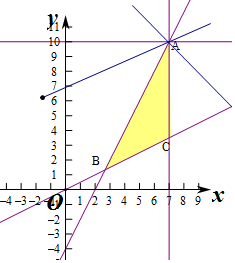 z=ax+y得y=-ax+z,
z=ax+y得y=-ax+z,
若a=0,则y=-ax+z,在A处取得最大值,此时最大值为10,不满足条件.
若a>0,即-a<0,此时在A处取得最大值,此时7a+10=7,即7a=-3,a=-$\frac{3}{7}$,不成立,
若a<0,即-a>0,此时在A处取得最大值,此时7a+10=7,即7a=-3,a=-$\frac{3}{7}$,
综上a=-$\frac{3}{7}$,
故答案为:-$\frac{3}{7}$,
点评 本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.抛物线y2=4x上有两点A,B到焦点的距离之和为7,则A,B到y轴的距离之和为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
14.椭圆的两个焦点分别为F1(-1,0)和F2(1,0),若该椭圆与直线x+y-3=0有公共点,则其离心率的最大值为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{6}}}{6}$-1 | C. | $\frac{{\sqrt{6}}}{12}$ | D. | $\frac{{\sqrt{5}}}{10}$ |
12.若将函数f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)图象上的每一个点都向左平移$\frac{π}{3}$个单位,得到g(x)的图象,则函数g(x)的单调递增区间为( )
| A. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | B. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$](k∈Z) | ||
| C. | [kπ-$\frac{2π}{3}$,kπ-$\frac{π}{6}$](k∈Z) | D. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) |