题目内容
13．抛物线y2=4x上有两点A，B到焦点的距离之和为7，则A，B到y轴的距离之和为（ ）| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
分析 根据抛物线的方程求出准线方程，利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离，列出方程求出A、B到y轴的距离之和．
解答 解：抛物线y2=4x的焦点F（1，0），准线方程x=-1
设A（x1，y1），B（x2，y2）
∴|AF|+|BF|=x1+1+x2+1=7
∴x1+x2=5，
∴A、B到y轴的距离之和为5，
故选：D．
点评 本题考查解决抛物线上的点到焦点的距离问题，解题的关键是利用抛物线的定义将到焦点的距离转化为到准线的距离．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
3．
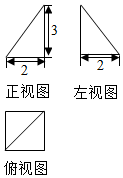已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）| A． | $\frac{4}{3}$cm3 | B． | $\frac{8}{3}$cm3 | C． | 2cm3 | D． | 4cm3 |
4．已知圆C1：x2+y2=4和圆2：（x-a）2+y2=4，其中a是在区间（0，6）上任意取得一个实数，那么圆C1和圆C2相交且公共弦长小于2$\sqrt{3}$的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{3}$ |
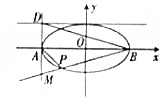如图，椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点分别为A，B，离心率为$\frac{\sqrt{2}}{2}$，直线x=-a与y=b交于点D，且|BD|=3$\sqrt{2}$，过点B作直线l交直线x=-a于点M，交椭圆于另一点P．
5．函数f（x）=$\frac{|x|}{\sqrt{1+{x}^{2}}\sqrt{4+{x}^{2}}}$的最大值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |