题目内容
11.在正方体ABCD-A1B1C1D1中,异面直线AD,BD1所成角的余弦值为$\frac{\sqrt{3}}{3}$.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AD,BD1所成角的余弦值.
解答 解: 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为1,
则A(1,0,0),D(0,0,0),B(1,1,0),D1(0,0,1),
$\overrightarrow{AD}$=(-1,0,0),$\overrightarrow{B{D}_{1}}$=(-1,-1,1),
设异面直线AD,BD1所成角为θ,
则cosθ=$\frac{|\overrightarrow{AD}•\overrightarrow{B{D}_{1}}|}{|\overrightarrow{AD}|•|\overrightarrow{B{D}_{1}}|}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
∴异面直线AD,BD1所成角的余弦值为$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{{\sqrt{3}}}{3}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )
| A. | 若α∥β,l∥α,则l?β | B. | 若α∥β,l⊥α,则 l⊥β | ||
| C. | 若α⊥β,l⊥α,则l?β | D. | 若α⊥β,l∥α,则 l⊥β |
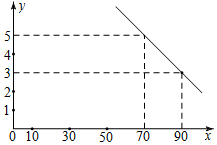 近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
近几年,由于环境的污染,雾霾越来越严重,某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎.已知这种口罩的进价为40元,经销过程中测出年销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售这种口罩的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.